如何快速进行度分秒、角度制与弧度制之间的换算?
在数学与物理的浩瀚宇宙中,度分秒、角度制与弧度制如同三座璀璨的灯塔,引领着探索者穿越理论与实践的海洋。无论你是学术研究的深度追求者,还是工程技术领域的实践者,掌握这三者之间的快速换算方法,都将是你解锁宇宙奥秘、提升工作效率的钥匙。今天,就让我们一起踏上一场奇妙的换算之旅,探索那些让人眼前一亮的技巧,让你的学习与工作如虎添翼。

度分秒:时间的痕迹,空间的密码
提到度分秒,大多数人首先想到的是时间的计量,但在几何与导航的世界里,它同样扮演着至关重要的角色。一度等于60分,一分等于60秒,这种十进制与六十进制的巧妙结合,让度分秒成为测量小角度变化的精准工具。想象一下,当你站在山巅,用望远镜精确测量远方山峰的倾斜角度,或是航海家利用星图与罗盘确定航线,度分秒的精确换算就是连接梦想与现实的桥梁。

快速换算小贴士:

将度转换为分秒:只需将度数乘以3600(因为60×60=3600),得到的即是总秒数。

将分秒转换回度:先将秒数除以60得到分数,再将分数与度数相加,或将总秒数直接除以3600得到度数。
角度制:直观易懂的几何语言
角度制,作为我们日常接触最多的角度表示方式,它的直观性和易用性无可替代。从直角三角形的直角,到圆周的360度完满,角度制以其简洁明了的方式,诠释了空间中的方向变化与大小关系。在建筑设计中,无论是屋顶的倾斜角度,还是门窗的定位,角度制都是设计师手中的得力助手。而在物理学中,角度制更是力学、光学等领域不可或缺的语言。
与度分秒的互动:
角度制与度分秒之间的转换,核心在于理解它们之间的进制关系,即1°=60′=3600″。
当你需要将一个精确到秒的角度值转换为更常用的度数形式时,不妨先将其转换为分,再除以60得到度数,余数即为分,同理可继续细分至秒。
弧度制:数学王国的优雅舞者
如果说角度制是几何世界的直观表达,那么弧度制则是数学与物理领域的深度对话。弧度制以圆的半径长度为基准,定义弧长与半径之比作为角度的度量。它之所以在数学中备受青睐,是因为它能够简化许多公式的形式,如三角函数、微积分中的导数与积分,使得运算过程更加流畅与自然。弧度制下,圆周角恰好等于2π,这一优雅的等式不仅揭示了圆的本质,也成为了连接三角函数与复数的桥梁。
快速换算的艺术:
角度制转弧度制:将角度值乘以π/180,即可得到对应的弧度值。例如,90°转换为弧度制就是π/2。
弧度制转角度制:将弧度值乘以180/π,即可得到对应的角度值。这种换算的关键在于掌握π与180之间的比例关系。
实战演练:掌握快速换算的秘诀
掌握了理论,接下来是实战演练的时刻。不妨尝试以下几个练习,将理论知识转化为实战技能:
1. 度分秒换算:将75°34′12″转换为度数形式。
解答:先将秒转换为分:12″=0.2′;再将得到的分与原有的分相加:34′+0.2′=34.2′;最后将分转换为度:34.2′=0.57°;所以,75°34′12″=75.57°。
2. 角度制转弧度制:将45°转换为弧度制。
解答:45°×π/180=π/4。
3. 弧度制转角度制:将π/3转换为角度制。
解答:π/3×180/π=60°。
深度理解:为何掌握换算如此重要?
1. 跨学科应用:无论你是天文学家计算行星轨道,还是程序员开发图形界面,甚至是艺术家在画布上描绘光影,度分秒、角度制与弧度制的快速换算都是必不可少的技能。
2. 提升计算效率:在复杂的数学与物理问题中,选择合适的角度单位可以极大地简化计算过程,减少错误率,提升解题效率。
3. 培养逻辑思维:掌握多种角度单位的换算,不仅是对数学公式的应用,更是对逻辑思维与问题解决能力的锻炼。它教会我们如何从不同角度审视问题,寻找最优解。
结语:开启无限可能的钥匙
在这场关于度分秒、角度制与弧度制的换算之旅中,我们不仅学会了如何快速准确地进行单位转换,更重要的是,我们学会了如何运用这些工具去探索未知,解决问题。它们不仅是数学与物理领域的基石,更是连接理论与实践、现实与梦想的桥梁。掌握了这些换算方法,你将能够在科学研究的浩瀚星空中自由翱翔,在工程技术的广阔天地间挥洒自如。让这把开启无限可能的钥匙,引领你走向更加辉煌的未来吧!
- 上一篇: 揭秘清明节的由来:一段鲜为人知的历史故事
- 下一篇: Win10电脑开机密码轻松设置与更改指南
-
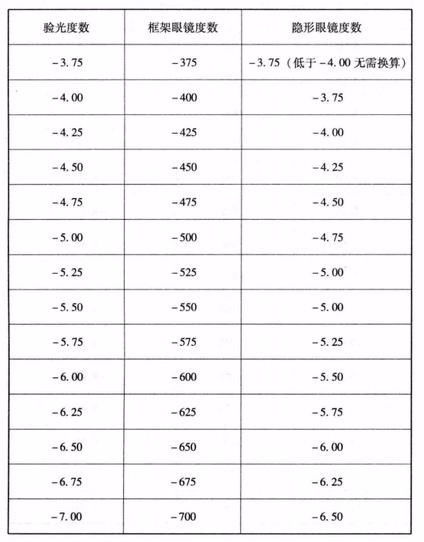 度分秒单位换算全攻略资讯攻略11-16
度分秒单位换算全攻略资讯攻略11-16 -
 揭秘角的换算奥秘:轻松掌握换算方法资讯攻略11-15
揭秘角的换算奥秘:轻松掌握换算方法资讯攻略11-15 -
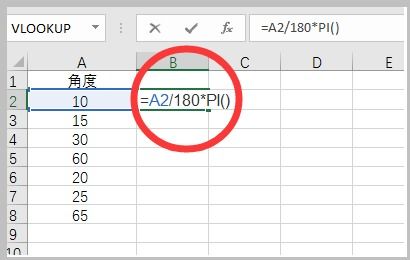 揭秘角度与弧度的魔法转换:公式大揭秘资讯攻略02-13
揭秘角度与弧度的魔法转换:公式大揭秘资讯攻略02-13 -
 96度伏特加相当于多少度白酒资讯攻略01-25
96度伏特加相当于多少度白酒资讯攻略01-25 -
 Excel高手必备:掌握SEC函数的高效使用技巧资讯攻略11-01
Excel高手必备:掌握SEC函数的高效使用技巧资讯攻略11-01 -
 一钱等于多少克黄金如何计算?资讯攻略02-14
一钱等于多少克黄金如何计算?资讯攻略02-14












