揭秘角度与弧度的魔法转换：公式大揭秘

在数学和物理学中，角度和弧度是两种用来度量角的大小的单位。虽然在日常生活中，我们更习惯于使用度数来表示角，但在科学计算和高级数学中，弧度制却显得尤为重要。本文将详细介绍角度与弧度之间的转换公式，以及它们在不同领域中的应用。

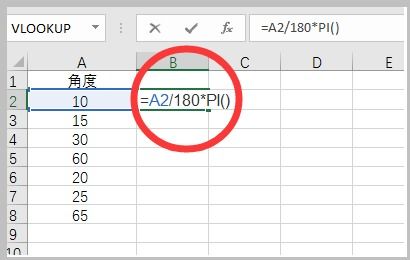
一、角度与弧度的基本概念

角度

角度（Degree）是度量角大小的常用单位，用符号“°”表示。一个完整的圆周被划分为360度。一个直角，即两条线垂直相交时所形成的角，被定义为90度。角度的度量方式直观易懂，因此广泛应用于日常生活和各种工程领域。

弧度

弧度（Radian）是另一种度量角大小的方式，它基于圆的半径。一个圆的周长与半径的比值被定义为2π（π约等于3.14159），而一个完整的圆周所对应的角度被定义为2π弧度，或简称为2π。因此，一个直角在弧度制下表示为π/2。弧度制在科学计算和高级数学中具有独特的优势，因为它使得许多数学公式和定理的表达更加简洁和直观。

二、角度与弧度的转换公式

角度转弧度

要将角度转换为弧度，可以使用以下公式：

弧度 = 角度 × π / 180

这个公式的推导基于一个完整圆周的角度和弧度之间的关系。由于一个圆周是360度，而对应的弧度是2π，因此可以通过比例关系得出上述转换公式。

例如，要将45度转换为弧度，可以计算：

弧度 = 45 × π / 180 = π / 4

弧度转角度

要将弧度转换为角度，可以使用以下公式：

角度 = 弧度 × 180 / π

这个公式的推导同样基于角度和弧度之间的比例关系。通过颠倒角度转弧度的公式，我们可以得出弧度转角度的公式。

例如，要将π/3弧度转换为角度，可以计算：

角度 = π / 3 × 180 / π = 60°

三、角度与弧度在不同领域中的应用

三角函数

在三角函数中，角度和弧度是两种常见的输入单位。三角函数，如正弦（sin）、余弦（cos）和正切（tan），是数学和物理学中的基础工具。在弧度制下，三角函数的性质和公式表达更加简洁和直观。例如，正弦函数的导数在弧度制下是cos(x)，而在角度制下则需要乘以一个额外的系数π/180。这使得弧度制在计算和推导三角函数公式时更加方便。

微积分

在微积分中，弧度制的应用同样广泛。微积分的基本概念和运算，如导数、积分和极限，都依赖于角度的度量单位。在弧度制下，这些运算的表达更加简洁和直观。例如，在计算圆的周长和面积时，弧度制使得公式更加简洁明了。此外，在求解涉及角度变化的微分方程时，弧度制也提供了更自然的表达方式。

物理学

在物理学中，角度和弧度都是重要的度量单位。特别是在力学、电磁学和量子力学等领域中，角度和弧度的转换和计算是不可或缺的。例如，在量子力学中，波函数的相位差通常使用弧度来表示；在力学中，旋转物体的角度变化也常用弧度来度量。

工程学

在工程学中，角度和弧度同样具有广泛的应用。特别是在机械、航空航天和建筑等领域中，角度的度量是设计、制造和安装过程中必不可少的环节。虽然在实际应用中，角度制可能更加直观和易于理解，但在进行精确计算和仿真时，弧度制通常更为方便和准确。

计算机科学

在计算机科学中，角度和弧度的转换和计算同样具有重要地位。特别是在图形学、动画和游戏开发中，角度和弧度的度量是渲染、动画和物理模拟的基础。在计算机程序中，角度和弧度的转换通常通过内置的数学函数来实现，如C语言的atan2函数用于计算反正切值并返回弧度结果。

四、角度与弧度转换的实际应用案例

案例一：机械设计中的角度计算

在机械设计中，经常需要计算旋转部件的角度变化。例如，在设计一个齿轮传动系统时，需要计算不同齿轮之间的角度关系以确保传动的准确性和效率。这时，角度和弧度的转换就显得尤为重要。通过将角度转换为弧度，可以更方便地应用三角函数来计算齿轮之间的相对位置和速度。

案例二：物理学中的运动学分析

在物理学中，运动学分析通常涉及物体的位置、速度和加速度等物理量的计算。当物体进行旋转运动时，其角度变化通常使用弧度来表示。例如，在分析一个绕固定轴旋转的刚体时，需要计算其角速度、角加速度和角动量等物理量。这些计算都依赖于角度和弧度的转换和计算。

案例三：计算机图形学中的渲染算法

在计算机图形学中，渲染算法通常涉及对三维场景中的物体进行投影和变换等操作。这些操作需要精确地计算物体的位置、方向和形状等参数。当物体进行旋转或倾斜等操作时，其角度变化也需要进行角度和弧度的转换和计算。通过精确的角度和弧度转换，可以确保渲染结果的准确性和真实性。

五、结论

角度和弧度是两种常用的度量角大小的单位，它们在数学、物理学、工程学、计算机科学等领域中具有广泛的应用。通过掌握角度与弧度之间的转换公式和计算方法，我们可以更方便地进行科学计算和工程设计。同时，了解角度和弧度在不同领域中的应用案例也有助于我们更好地理解它们的实际应用价值和意义。因此，在学习和实践过程中，我们应该注重角度和弧度的转换和应用能力的培养，以更好地应对各种挑战和问题。