揭秘整数的奥秘

整数是数学中基础而重要的概念，它是数的一种表现形式，用于表示没有小数部分的数。在数学的发展历程中，整数的概念逐渐从具体的计数需求中抽象出来，成为数学体系中的基石。本文将从整数的定义、性质、运算以及在实际生活中的应用等多个方面，深入探讨整数的奥秘。

首先，我们需要明确整数的定义。整数包括正整数、零和负整数。正整数就是我们通常所说的1、2、3、...等，用于表示物体的数量或顺序。零是一个特殊的整数，它既不是正数也不是负数，而是整数的分界点。负整数则是正整数的相反数，如-1、-2、-3、...等，用于表示欠债、温度下降等具有相反意义的量。整数集通常用符号Z表示，其中Z来源于德语Zahlen（数）的首字母。

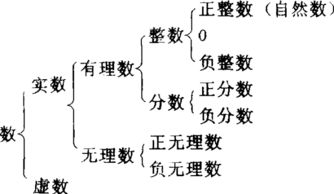
整数的性质是其区别于其他数的重要特征。首先，整数具有封闭性，即任意两个整数相加、相减、相乘的结果仍然是整数。这一性质保证了整数在运算过程中的稳定性。其次，整数具有序性，即可以比较大小。对于任意两个整数a和b，要么a大于b，要么a小于b，要么a等于b。这一性质使得整数能够用于表示顺序和数量关系。此外，整数还具有整除性，即一个整数a能被另一个整数b整除（b≠0），当且仅当存在一个整数c，使得a=bc。整除性是整数的一个重要性质，它为我们判断两个整数之间的数量关系提供了依据。

整数的运算包括加法、减法、乘法和除法。整数的加法满足交换律和结合律，即a+b=b+a和(a+b)+c=a+(b+c)。整数的减法可以看作加法的逆运算，即a-b=a+(-b)。整数的乘法同样满足交换律、结合律和分配律，即ab=ba、(ab)c=a(bc)和a(b+c)=ab+ac。整数的除法则需要特别注意，因为不是所有整数都能被另一个整数整除。当a能被b整除时，我们称a是b的倍数，b是a的因数。此时，我们可以说a除以b的商是c，余数是0。当a不能被b整除时，我们得到的是一个商和一个非零余数。

整数在实际生活中有着广泛的应用。在计数方面，整数用于表示物体的数量，如人口数量、书籍数量等。在排序方面，整数用于表示顺序，如成绩排名、比赛名次等。在测量方面，整数用于表示长度、重量等物理量的近似值，如房间的长度约为5米、物体的重量约为10千克等。此外，整数还广泛应用于计算机科学、金融、物理学等领域。在计算机科学中，整数是数据类型的基本元素之一，用于存储和处理各种数值信息。在金融领域，整数用于表示货币金额、交易量等经济指标。在物理学中，整数用于描述量子态、振动模式等物理现象。

除了基本运算外，整数还有一些特殊的性质和运算规律。例如，奇数和偶数是整数的一个重要分类。奇数是不能被2整除的整数，如1、3、5等；偶数则是能被2整除的整数，如0、2、4等。奇数和偶数具有一些特殊的性质，如奇数+奇数=偶数、偶数+偶数=偶数、奇数+偶数=奇数等。此外，整数还有素数、合数等分类。素数是指只有1和它本身两个正因数的整数，如2、3、5等；合数则是指除了1和它本身外还有其他正因数的整数，如4、6、8等。素数在数论和密码学中有着广泛的应用。

在整数的研究中，还有一些经典的数学问题和定理。例如，哥德巴赫猜想是一个关于素数的著名猜想，它提出：任何大于2的偶数都可以表示为两个素数之和。尽管这个猜想尚未被证明或证伪，但它激发了数学家们对素数分布和性质的深入研究。另一个著名的定理是费马小定理，它指出：如果p是一个质数，a是一个整数且a不被p整除，那么a的p-1次方模p余1。费马小定理在数论和密码学中有着广泛的应用，特别是在设计加密算法时。

此外，整数还与分数、小数等其他数有着密切的关系。分数是表示有理数的另一种形式，它表示两个整数的比。小数则是十进制的另一种表示形式，它可以通过有限小数或无限循环小数来表示有理数。整数、分数和小数在数学中共同构成了有理数的完整体系。

随着数学的发展，整数的研究也不断深入。现代数学中的代数、数论、组合数学等领域都对整数进行了广泛的研究。代数中的多项式理论、同余理论等与整数密切相关；数论中的素数分布、素数定理等研究深化了我们对整数的认识；组合数学中的排列组合、图论等也与整数有着紧密的联系。这些研究不仅推动了数学的发展，也为其他学科提供了有力的数学工具。

综上所述，整数是数学中基础而重要的概念。它具有明确的定义和丰富的性质，能够用于表示数量、顺序和关系等数学概念。整数的运算规律简单明了，广泛应用于实际生活中。同时，整数还与分数、小数等其他数有着密切的关系，共同构成了有理数的完整体系。随着数学的发展，整数的研究也不断深入，为其他学科提供了有力的数学支持。因此，深入理解和掌握整数的概念和性质对于我们学好数学、解决实际问题具有重要意义。