如何进行因式分解？

在进行数学学习的旅程中，有一个非常实用且常见的技巧，那就是“因式分解”。简单来说，因式分解就是把一个多项式表达式转化为几个整式的乘积形式。它不仅是学习代数的基础，也是解决很多数学问题，比如方程求解、不等式分析等的关键步骤。下面，我们就来详细探讨一下怎么进行因式分解，以及在这个过程中的一些技巧和注意事项。

首先，我们需要明确什么是多项式。多项式是由数字、未知数（通常用字母表示，如x、y等）以及运算符号（加、减、乘）构成的代数式。例如，3x² + 4x - 5就是一个多项式。当我们需要对这样的多项式进行因式分解时，目标就是找到一些更简单的整式，通过它们的乘积能够重新得到原来的多项式。

一、基本步骤与策略

1. 提取公因式

这是因式分解中最基础也是最常见的一步。如果一个多项式的各项都含有某个相同的因子（可以是数字或未知数），那么我们就可以把这个公共因子提取出来，放在括号外面，剩下的部分作为新的多项式。例如，在3x² + 6x中，3x是公共因子，提取后得到3x(x + 2)。

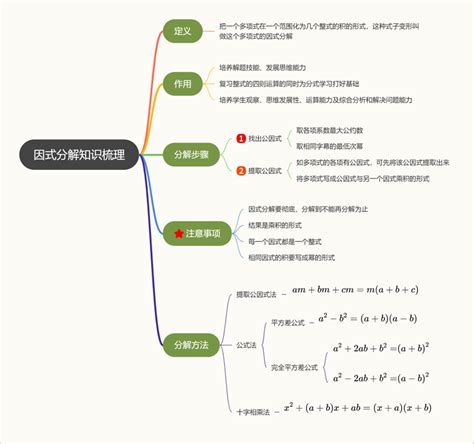
2. 公式法

对于一些特殊形式的多项式，我们可以直接使用已知的因式分解公式。比如，平方差公式a² - b² = (a + b)(a - b)和完全平方公式a² + 2ab + b² = (a + b)²。利用这些公式，我们可以快速地对相应的多项式进行因式分解。

3. 十字相乘法

这是一种适用于二次多项式（形如ax² + bx + c）的因式分解方法。虽然它的名字听起来有些复杂，但实际操作起来却相当直观。我们需要找到两个数，它们的乘积等于首项系数与常数项的乘积（即ac），且它们的和等于中间项的系数（即b）。一旦找到这两个数，就可以将它们分别作为两个一次式的系数，从而得到原多项式的因式分解形式。

4. 分组分解法

当多项式项数较多，且没有明显的公因式或适合直接使用公式的情况时，我们可以尝试将多项式分成几组，然后分别对各组进行因式分解，最后再将结果组合起来。这种方法虽然比较灵活，但也更考验观察力和逻辑推理能力。

二、实际应用与注意事项

1. 方程求解

因式分解在解一元二次方程（形如ax² + bx + c = 0）时尤为重要。通过将方程左侧的多项式进行因式分解，我们可以将其转化为两个一次式的乘积等于0的形式，从而轻松地找到方程的解。

2. 不等式分析

在解决一些不等式问题时，因式分解同样能帮助我们简化问题。通过分解多项式，我们可以更容易地找到不等式的临界点（即多项式等于0的点），进而分析不等式的解集。

3. 函数性质研究

在函数学习中，因式分解也是研究函数性质的重要工具。例如，通过分解多项式函数，我们可以确定函数的零点（即函数值为0的点），进而分析函数的单调性、极值等性质。

注意事项：

耐心观察：因式分解往往需要一些试错和观察的过程。不要急于求成，耐心分析多项式的结构，寻找可能的因式分解途径。

灵活运用：不同的多项式可能需要不同的因式分解策略。有时候，一种方法行不通，不妨试试另一种。灵活运用各种因式分解技巧是解决问题的关键。

检查验证：完成因式分解后，一定要记得将分解后的整式乘积重新展开，与原多项式进行对比验证，确保分解的正确性。

三、实战演练

让我们通过几个具体的例子来练习一下因式分解：

例1：分解多项式4x² - 9

解答：这是一个平方差形式的多项式，可以直接应用平方差公式进行分解。得到：

4x² - 9 = (2x)² - 3² = (2x + 3)(2x - 3)

例2：分解多项式x² - 5x + 6

解答：这是一个二次多项式，尝试使用十字相乘法。我们需要找到两个数，它们的乘积为6（即首项系数1与常数项6的乘积），且它们的和为-5（即中间项的系数）。这两个数分别是-2和-3。因此，多项式可以分解为：

x² - 5x + 6 = (x - 2)(x - 3)

例3：分解多项式6x³ - 3x² - 12x

解答：首先提取公因式3x，得到：

6x³ - 3x² - 12x = 3x(2x² - x - 4)

接着，对括号内的二次多项式进行十字相乘法分解（虽然这里并不直接适用，但我们可以尝试将其视为不完全的因式分解，并寻找可能的简化路径）。不过，在这个例子中，更直接的做法是观察到2x² - x - 4可以进一步分解为(2x + 3)(x - 4)（通过尝试或更高阶的因式分解技巧）。因此，最终分解为：

6x³ - 3x² - 12x = 3x(2x + 3)(x - 4)

通过上面的例子，我们可以看到因式分解不仅需要对基本技巧熟练掌握，还需要一定的观察力和逻辑推理能力。随着实践的积累，你会逐渐发现因式分解的乐趣和它在数学学习中的广泛应用。

总之，因式分解是数学学习中的一项基本技能，它不仅能够简化复杂的数学表达式，还能帮助我们更深入地理解数学问题的本质。希望这篇文章能够帮助你掌握因式分解的基本方法和技巧，让你在数学学习的道路上更加得心应手。