常微分方程的通解公式是什么？

揭秘常微分方程通解公式：探索数学世界的钥匙

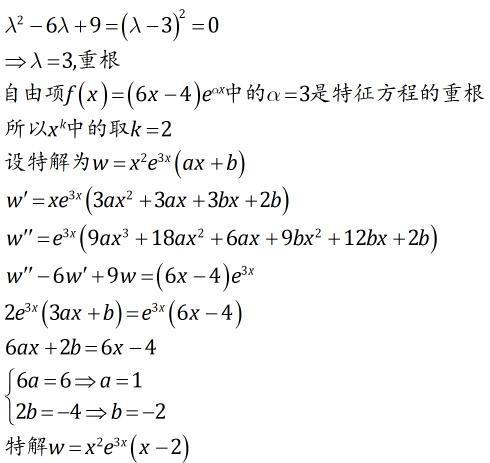
在数学的浩瀚宇宙中，常微分方程（ODE）如同一座神秘的宝库，蕴藏着自然界与工程领域无数规律的秘密。它描述了一个或多个未知函数及其导数之间的关系，而这些关系往往揭示了现实世界中的动态过程。当我们试图解开这些方程的谜团，寻找它们的通解时，一个关键的公式——常微分方程通解公式，便如同一把开启宝库的钥匙，引领我们进入知识的殿堂。

初识常微分方程

首先，让我们简单回顾一下常微分方程的基本概念。一个常微分方程是包含未知函数（通常是时间的函数）及其导数（或更高阶导数）的等式。如果方程中只涉及未知函数的一阶导数，我们称之为一阶常微分方程；若涉及更高阶的导数，则相应地称为二阶、三阶或更高阶的常微分方程。

例如，一个简单的一阶常微分方程可能是这样的：dy/dx = 2x + 3，其中y是未知函数，x是自变量，dy/dx表示y关于x的一阶导数。

通解与特解

在探讨常微分方程的通解公式之前，有必要先明确两个重要概念：通解和特解。

特解：是满足方程及其特定初始条件（或边界条件）的解。特解是方程解集中的一个具体成员，它提供了方程在某个特定情境下的精确答案。

通解：则是一个包含任意常数（或参数）的表达式，它描述了方程所有可能的解。通过为这些常数赋予特定的值，我们可以从通解中得出无数个特解。

通解的重要性在于，它为我们提供了一个框架，使我们能够系统地分析和理解方程的所有可能行为。

走进通解公式

现在，让我们正式揭开常微分方程通解公式的神秘面纱。值得注意的是，不同类型的常微分方程具有不同的通解公式，这里我们将重点介绍几种常见的类型及其通解公式。

一阶线性常微分方程

一阶线性常微分方程是最简单也是最常见的一类，其一般形式为：dy/dx + P(x)y = Q(x)，其中P(x)和Q(x)是关于x的已知函数。

对于这类方程，我们有一个非常有效的通解公式，即所谓的“积分因子法”。首先，我们找到一个积分因子μ(x)，使得乘以μ(x)后的方程变为一个可分离变量的方程。积分因子μ(x)通常是通过求解μ'(x) = μ(x)P(x)来得到的。一旦找到μ(x)，我们就可以将原方程两边同时乘以μ(x)，然后通过积分求解。

最终，一阶线性常微分方程的通解可以表示为：y = e^(-∫P(x)dx)[∫Q(x)e^(∫P(x)dx)dx + C]，其中C是任意常数。

可分离变量的方程

另一类常见的常微分方程是可分离变量的方程，其一般形式为：M(y)dy = N(x)dx，其中M(y)和N(x)是关于y和x的已知函数。

对于这类方程，通解公式相对简单直接。我们只需将方程两边分别积分，得到：∫M(y)dy = ∫N(x)dx + C，其中C是任意常数。通过解这个积分方程，我们可以找到y关于x的通解。

齐次方程

齐次方程是一种特殊形式的一阶常微分方程，其一般形式为：dy/dx = f(y/x)。这类方程可以通过令u = y/x进行换元，转化为一个关于u的可分离变量的方程。

通过求解转化后的方程，我们可以找到u关于x的表达式，进而通过u = y/x求出y关于x的通解。

二阶常系数线性齐次方程

对于二阶常系数线性齐次方程，其一般形式为：ay'' + by' + cy = 0，其中a、b和c是常数，y是关于x的未知函数。

这类方程的通解可以通过求解其特征方程λ² + bλ + c = 0来得到。特征方程的根λ1和λ2决定了方程的通解形式。具体来说，如果λ1和λ2是两个不相等的实数根，则通解为y = C1e^(λ1x) + C2e^(λ2x)；如果λ1和λ2是两个相等的实数根，则通解为y = (C1 + C2x)e^(λ1x)；如果λ1和λ2是一对共轭复数根α ± βi，则通解为y = e^(αx)(C1cosβx + C2sinβx)。

通解公式的魅力与挑战

常微分方程通解公式不仅揭示了方程解的结构，还为我们提供了一种系统化的方法来求解这类方程。通过应用这些公式，我们可以从复杂的数学表达式中抽象出简洁而深刻的物理意义，进而理解和预测现实世界中的动态过程。

然而，通解公式的应用也并非总是那么直观和简单。对于某些复杂的非线性方程或变系数方程，我们可能无法直接找到通解公式，甚至可能无法确定方程是否有解。在这种情况下，我们需要借助数值方法、近似方法或特殊技巧来求解方程。

此外，即使我们能够找到通解公式，也可能需要面对另一个挑战：如何从众多可能的解中选择出符合实际情境的那一个。这通常需要我们结合问题的物理背景、初始条件或边界条件来进行筛选和判断。

结语

常微分方程通解公式是数学领域的一颗璀璨明珠，它以其独特的魅力和广泛的应用价值吸引着无数数学爱好者和科学家的目光。通过学习和掌握这些公式，我们可以更加深入地理解自然界的奥秘，探索工程领域的未知领域。同时，我们也应该意识到，通解公式并非万能的钥匙，它需要我们结合具体问题和实际情况进行灵活运用和判断。只有这样，我们才能真正领略到数学世界的无限魅力和无穷奥秘。