探索逻辑电路的基石:与门、或门、非门与异或门的奥秘
在电子工程与计算机科学领域中,逻辑门是构成数字电路的基本单元,它们如同数字世界的“决策者”,通过特定的输入信号来产生相应的输出信号。其中,与门、或门、非门和异或门是最为基础且重要的四种逻辑门电路,它们各自拥有独特的逻辑功能和广泛的应用场景。本文将从定义、符号、真值表、逻辑表达式、电路实现以及实际应用等多个维度,深入解析这四种逻辑门。

与门(AND Gate)
定义:与门是一种数字逻辑门,仅当所有输入均为高电平(逻辑“1”)时,输出才为高电平(逻辑“1”);否则,输出为低电平(逻辑“0”)。这一特性反映了逻辑上的“与”关系,即所有条件同时满足时,结果才为真。
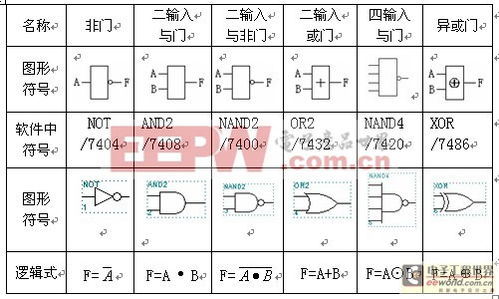
符号:与门的标准符号是一个带有输入端和输出端的矩形,其中输入端通过小圆圈相连,表示只有当所有输入均为1时,输出才为1。
真值表:对于一个双输入与门(A和B),其真值表如下:
| A | B | 输出 |
||||
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
逻辑表达式:与门的逻辑表达式为 A·B 或 AB(在某些文献中省略点乘符号)。这直观表达了只有当A和B都为1时,输出才为1的逻辑关系。
电路实现:在电子电路中,与门通常通过二极管、晶体管或集成逻辑芯片实现。例如,使用NPN型晶体管的串联配置可以模拟与门功能,当且仅当两个输入均为高电平时,输出端才会被拉低至高电平(考虑反相输出的情况)。
实际应用:与门广泛应用于需要多个条件同时满足才能触发事件的场景,如安全系统中的多重身份验证、数字锁的逻辑控制等。
或门(OR Gate)
定义:或门是另一种基本的逻辑门,只要有一个或多个输入为高电平(逻辑“1”),输出即为高电平(逻辑“1”);只有当所有输入均为低电平(逻辑“0”)时,输出才为低电平(逻辑“0”)。这反映了逻辑上的“或”关系,即至少一个条件满足时,结果即为真。
符号:或门的符号与与门类似,但输入端的小圆圈缺失,表明只要有一个输入为1,输出就为1。
真值表:对于双输入或门(A和B),其真值表如下:
| A | B | 输出 |
||||
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
逻辑表达式:或门的逻辑表达式为 A+B,表示A或B任一为1时,输出为1。
电路实现:或门可以通过二极管的并联或晶体管的并联配置实现。当任何一个输入为高电平时,都能使输出端达到高电平状态。
实际应用:或门常用于需要至少一个条件满足即可触发事件的场景,如灯光控制系统的多路开关、故障报警系统的任一传感器触发等。
非门(NOT Gate)
定义:非门是最简单的逻辑门,它只有一个输入和一个输出,输出是输入的逻辑反相。即,当输入为高电平(逻辑“1”)时,输出为低电平(逻辑“0”);反之亦然。这反映了逻辑上的“非”关系,即条件的否定。
符号:非门的符号为一个带有圆圈的小三角形或倒置的三角形,圆圈表示反相作用。
真值表:对于单输入非门(A),其真值表极为简单:
| A | 输出 |
|||
| 0 | 1 |
| 1 | 0 |
逻辑表达式:非门的逻辑表达式为¬A或A',表示A的逻辑非。
电路实现:非门可以通过NPN型晶体管或CMOS反相器实现。在CMOS技术中,一个P型MOSFET和一个N型MOSFET串联构成反相器,当输入变化时,两个晶体管交替导通和截止,从而实现输出对输入的反相。
实际应用:非门常用于信号的反转、逻辑状态的切换等,是数字电路设计中不可或缺的组成部分。
异或门(XOR Gate)
定义:异或门是一种双输入逻辑门,当且仅当两个输入不同(一个为1,另一个为0)时,输出为高电平(逻辑“1”);如果两个输入相同(均为0或均为1),输出为低电平(逻辑“0”)。这反映了逻辑上的“异或”关系,即两个条件不同则为真。
符号:异或门的符号是在或门符号的基础上增加一个额外的圆圈,表示输出的特殊条件。
真值表:对于双输入异或门(A和B),其真值表如下:
| A | B | 输出 |
||||
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
逻辑表达式:异或门的逻辑表达式较为复杂,常用A⊕B或A·¬B+¬A·B表示,即A与B的非的乘积加上A的非与B的乘积。
电路实现:异或门可以通过多个基本逻辑门的组合(如与门、或门和非门)实现,或者使用专门的XOR集成电路芯片。在CMOS技术中,异或门通常由四个晶体管构成,通过巧妙的连接实现其功能。
实际应用:异或门在加密解密、错误检测码(如奇偶校验)、数字通信等领域有着广泛应用。例如,在CRC(循环冗余校验)算法中,异或运算用于生成和验证数据的完整性校验码。
综上所述,与门、或门、非门和异或门作为数字逻辑的基础元件,各自承担着不同的逻辑运算任务,它们通过不同的组合方式,构建了复杂多样的数字电路系统。理解这些逻辑门的工作原理和应用场景,对于深入学习数字电路设计和计算机科学至关重要。随着技术的进步,虽然现代集成电路中可能集成了数以亿计的晶体管,但这些基本的逻辑门概念仍然是理解现代电子设备和计算机系统工作原理的基石。
- 上一篇: 揭秘蚂蚁庄园:哪种动物竟能“睁一只眼闭一只眼”睡觉?
- 下一篇: 自制花肥的简易方法大揭秘
-
 探索数字世界的基石:位、字节、字与字长的奥秘资讯攻略12-01
探索数字世界的基石:位、字节、字与字长的奥秘资讯攻略12-01 -
 揭秘:“皮”字的偏旁之谜资讯攻略11-18
揭秘:“皮”字的偏旁之谜资讯攻略11-18 -
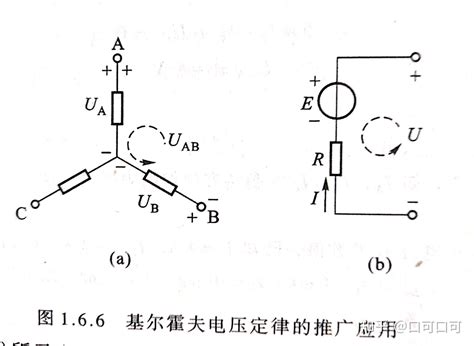 揭秘电学奥秘:深入解读基尔霍夫第二定律资讯攻略02-22
揭秘电学奥秘:深入解读基尔霍夫第二定律资讯攻略02-22 -
 揭秘:基尔霍夫第一定律的奥秘资讯攻略11-21
揭秘:基尔霍夫第一定律的奥秘资讯攻略11-21 -
 电桥法测量电阻的奥秘解析资讯攻略01-25
电桥法测量电阻的奥秘解析资讯攻略01-25 -
 时间继电器的作用是什么?资讯攻略11-29
时间继电器的作用是什么?资讯攻略11-29









