高斯如何构造正十七边形的做法是什么？

探索数学史上的奇迹：高斯的正十七边形做法

在数学的浩瀚星空中，高斯（Johann Carl Friedrich Gauss）无疑是一颗璀璨的明星。他不仅在数学领域有着卓越的贡献，还在物理学、天文学等多个学科留下了深刻的印记。而在高斯的众多数学成就中，他关于正十七边形的构造方法无疑是一段传奇。这一方法不仅展示了高斯深厚的数学功底，也揭示了数学之美与实用性的完美结合。

高斯的数学背景与成就

高斯生于1777年，逝于1855年，是德国著名的数学家、物理学家、天文学家和大地测量学家。他自幼便展现出非凡的数学天赋，年仅三岁便能纠正父亲的算术错误。高斯在年轻时便独立发现了二项式定理的一般形式，并解决了困扰数学家们已久的正十五边形和正十七边形的尺规作图问题。他的这些成就，即使是在数学史上也堪称奇迹。

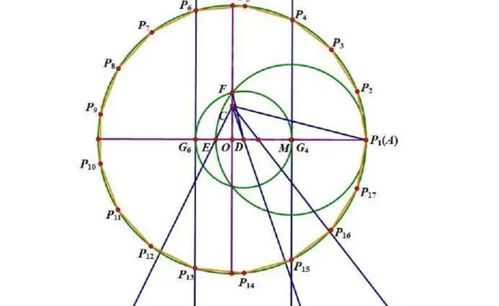
高斯的数学研究覆盖了数论、代数、几何、分析等多个领域。他提出了高斯定理、高斯和、高斯函数等重要概念，对微积分的严格化也做出了重要贡献。此外，高斯在概率论、矩阵论、复变函数论等方面也有着开创性的工作。他的数学天赋和成就，使他被誉为“数学王子”。

正十七边形的尺规作图问题

尺规作图是古希腊数学家们研究的一个重要问题。他们试图仅用无刻度的直尺和圆规来作出各种几何图形。然而，并非所有的几何图形都能通过尺规作图来构造。正十七边形便是一个长期困扰数学家们的难题。

早在古希腊时期，数学家们就已经知道如何构造正三边形、正方形、正五边形等简单多边形。然而，对于正十七边形这样的复杂多边形，他们却束手无策。这一难题一直悬而未决，直到高斯的出现。

高斯的解题思路与过程

高斯在解决正十七边形的尺规作图问题时，采用了代数与几何相结合的方法。他首先证明了正十七边形可以用尺规作图构造出来，然后给出了具体的构造步骤。

高斯的关键突破在于他发现了正十七边形的边长与半径之间的特殊关系。他通过代数方法证明了存在一个多项式，其根与正十七边形的边长和半径有关。这个多项式便是著名的十七次单位根多项式。

高斯进一步指出，可以通过尺规作图的方法逐步求出这个多项式的根，从而构造出正十七边形的边长和顶点。他的具体构造过程涉及到了复杂的几何变换和代数运算，但最终成功地作出了正十七边形。

尺规作图的具体步骤

虽然高斯的证明过程涉及到了高深的代数知识，但他的构造方法却可以通过简单的几何操作来实现。以下是一个简化的尺规作图步骤，用于构造正十七边形：

1. 作圆与直径：首先，在纸上作出一个圆O，并标出圆心。然后，通过圆心作一条直径AB。

2. 确定单位长度：在直径AB上取一点C，使得AC的长度等于圆的半径。接着，以C为圆心、AC为半径作一个小圆。这个小圆与圆O在A点相切。

3. 构造黄金分割：通过A点作一条与直径AB垂直的直线l。在直线l上取一点D，使得AD的长度等于小圆的半径。然后，连接CD并延长至与圆O相交于点E。点E便是黄金分割点之一。

4. 求十七次单位根：接下来是一个复杂的代数与几何结合的过程。高斯通过一系列几何变换和代数运算，逐步求出了十七次单位根多项式的根。这些根对应着正十七边形的边长和顶点。具体的构造步骤涉及到了多个辅助圆、辅助线和几何变换，这里不再赘述。

5. 作出正十七边形：在求出所有十七次单位根后，高斯便可以在圆O上标出正十七边形的所有顶点。连接这些顶点，便得到了一个完美的正十七边形。

高斯方法的意义与影响

高斯关于正十七边形的尺规作图方法不仅解决了长期困扰数学家们的难题，也展示了数学之美与实用性的完美结合。他的方法不仅在数学领域引起了轰动，也激发了人们对数学和科学的热爱与追求。

高斯的方法证明了尺规作图的强大能力，同时也揭示了代数与几何之间的深刻联系。他的这一成就为后来的数学家们提供了宝贵的启示和借鉴。许多数学家在高斯的基础上进一步研究了尺规作图问题和其他几何问题，推动了数学和几何学的发展。

此外，高斯的方法也激发了人们对数学美的追求。正十七边形的构造过程不仅展示了数学的严谨性和精确性，也体现了数学的对称性和和谐性。这种美在数学和艺术领域都有着广泛的应用和影响。

结语

高斯关于正十七边形的尺规作图方法是数学史上的一段传奇。它不仅解决了长期困扰数学家们的难题，也展示了数学之美与实用性的完美结合。高斯的方法不仅在数学领域产生了深远的影响，也激发了人们对数学和科学的热爱与追求。他的这一成就将永远铭刻在数学史上，成为人类智慧的瑰宝。

在当今时代，数学仍然是一门充满挑战和机遇的学科。高斯的方法和思想仍然激励着数学家们不断探索和创新。我们相信，在未来的数学研究中，人们将继续发现更多的数学之美和实用之处，为人类的进步和发展做出更大的贡献。