圆的面积计算公式是如何推导出来的?
圆,作为几何学中最基本的形状之一,自古以来就吸引着无数数学家和学者的目光。其面积的计算,更是几何学研究中的一个重要课题。圆的面积推导公式,不仅在数学领域有着广泛的应用,而且在整个自然科学和工程技术中,都扮演着举足轻重的角色。本文将围绕“圆的面积推导公式是什么”这一主题,深入探讨其历史背景、推导过程以及实际应用。
早在古代,人们就开始对圆的面积进行探索。古希腊数学家阿基米德,被誉为“力学之父”,他通过一系列巧妙的几何构造,逼近了圆的面积。阿基米德的方法虽然原始,却蕴含了微积分的思想萌芽,为后来科学家推导圆的面积公式奠定了坚实的基础。在中国,古代数学家刘徽在《九章算术注》中,也提出了用内接和外切正多边形逼近圆的方法,来估算圆的面积,这一思路与阿基米德的方法不谋而合。
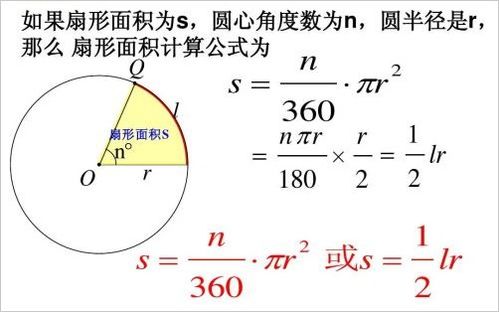
那么,圆的面积推导公式究竟是什么呢?在平面几何中,一个半径为r的圆的面积S,可以用公式S=πr²来计算。这个公式简洁而优美,但它背后的推导过程却充满了智慧和匠心。

一种常见的推导方法,是利用圆的切线与半径构成的直角三角形。想象一个圆,从圆心出发画一条半径,再在这条半径的末端画一条切线,切线与过圆心的某条直径相交于一点。这样,我们就得到了一个直角三角形,其中一个直角边是半径r,另一个直角边是从切点到直径与切线交点的线段,记为l。根据勾股定理,我们可以知道l²+r²等于直径的平方,也即4r²(因为直径是半径的两倍)。但由于l是从切点到直径与切线交点的线段,它实际上等于圆上从切点沿圆周移动到与直径相对的另一切点所经过的弧长的一半(这是因为在很小的一段弧上,弧长近似等于弦长)。所以,我们可以将l看作是圆周长的一小部分,而圆的周长C=2πr。因此,l≈(πr/2πr)×C=r(这里的近似是基于弧长与弦长在极小段上的等价性)。将这个结果代入勾股定理得到的等式中,并考虑到当我们将圆分割成越来越多的这样的小直角三角形时,它们的面积之和将越来越接近圆的面积,我们可以发现,每个小直角三角形的面积(1/2)×r×l累加起来,就得到了圆的面积。而由于l≈r(在极限情况下),所以每个小三角形的面积近似为(1/2)r²,当我们将这些小三角形的面积加在一起时,它们的数量(即圆的周长与半径的比值,也即2π)乘以每个小三角形的面积,就得到了圆的面积公式S=πr²。
当然,上述推导过程是一种直观而启发式的理解,它依赖于对极限概念的直观感受。在现代数学中,我们通常利用微积分来严格推导圆的面积公式。通过将圆分割成无数细小的扇形,每个扇形的面积可以看作是矩形(其底为扇形的弧长,高为圆的半径)的面积的近似。当我们将这些细小的扇形面积加在一起时,它们的和就趋近于圆的面积。而扇形的弧长与圆的半径的比值,在极限情况下就是扇形的中心角(以弧度为单位)与2π的比值。因此,通过将整个圆的面积看作是所有扇形面积的和,并利用积分的概念,我们可以严格推导出圆的面积公式S=πr²。
圆的面积推导公式不仅在理论上具有重要意义,而且在实际应用中也有着广泛的用途。在工程设计中,当我们需要计算管道、轮毂等圆形构件的面积时,圆的面积公式是必不可少的工具。在物理学中,圆的面积公式与圆周运动、波动等现象密切相关。在天文学中,行星轨道、恒星表面等都与圆的面积有关。此外,在统计学、经济学等领域,圆的面积公式也有着重要的应用。例如,在统计学中,我们经常需要计算数据的离散程度,而圆的面积公式可以帮助我们理解数据的分布特征。在经济学中,圆的面积公式可以用于计算生产成本、市场份额等经济指标。
值得一提的是,圆的面积公式中的π是一个神秘的常数,它约等于3.14159...。π的发现和研究历程充满了传奇色彩。从古希腊数学家阿基米德开始,无数数学家为求解π的精确值而绞尽脑汁。他们发明了各种巧妙的方法来计算π,如阿基米德的几何方法、刘徽的“割圆术”、祖冲之和祖暅的“缀术”等。随着计算机的发展,人们已经能够计算出π的数十亿位小数。但尽管如此,π的本质和性质仍然吸引着数学家们的关注和研究。
圆的面积推导公式是几何学中的一颗璀璨明珠。它不仅揭示了圆的面积与半径之间的内在联系,而且为整个自然科学和工程技术的发展提供了有力的数学支持。通过对圆的面积推导公式的深入研究和理解,我们可以更好地把握自然界的奥秘和规律,推动人类文明的进步和发展。在未来的科学研究中,圆的面积公式将继续发挥着不可替代的作用,引领我们探索未知的世界。
- 上一篇: 怎样在韩国网站上观看视频?
- 下一篇: 首次清洗新牛仔裤的正确方法
-
 半圆面积的计算公式是什么?资讯攻略10-29
半圆面积的计算公式是什么?资讯攻略10-29 -
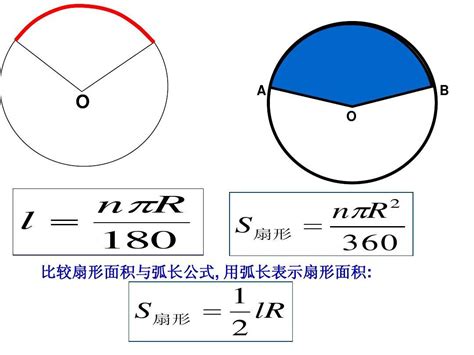 扇形面积如何计算?资讯攻略11-27
扇形面积如何计算?资讯攻略11-27 -
 长方体表面积的计算公式是什么?资讯攻略02-06
长方体表面积的计算公式是什么?资讯攻略02-06 -
 高中扇形弧长与面积计算公式详解资讯攻略11-10
高中扇形弧长与面积计算公式详解资讯攻略11-10 -
 六年级学生如何计算半圆周长公式资讯攻略11-06
六年级学生如何计算半圆周长公式资讯攻略11-06 -
 球的表面积计算公式及详解资讯攻略11-25
球的表面积计算公式及详解资讯攻略11-25












