明确区分:因数与倍数的差异与识别方法
在数学的广阔天地里,因数和倍数作为基石般的概念,不仅构建了数的性质与关系,还深刻影响着代数、几何等多个领域。对于初学者而言,准确区分因数和倍数,是掌握数学基础、提升逻辑思维能力的关键一步。本文将深入浅出地探讨如何有效区分这两个看似相似实则迥异的概念,帮助读者在数的海洋中导航,增强对数学知识的理解和应用能力。

一、定义初探:揭开因数和倍数的面纱
因数:若整数a能被整数b整除(b不为0),则称b是a的因数,或a是b的倍数。简而言之,因数就是能够整除给定数的那些数。例如,12的因数有1、2、3、4、6、12,因为这些数都能被12整除,没有余数。
倍数:一个数能够被另一数整除时,这个数就是另一数的倍数。换个说法,倍数是基于因数的概念反向定义的,它表示的是某个数通过重复加自身(或其因数)若干次得到的数。继续以12为例,2的倍数有2、4、6、8、10、12...等,因为这些都是2不断加自己或乘以某个整数得到的。
二、核心区别:寻找因数和倍数的差异
1. 视角不同
因数:从被除数(或说被考察的数)出发,寻找能整除它的数。这是一个“向内看”的过程,关注的是哪些数能构成该数的“组成部分”。
倍数:则是从一个给定的数(通常是较小的数)出发,探索它通过乘法可以扩展到的所有数。这是一个“向外扩展”的过程,展现了一个数如何通过重复自身或与其他数相乘来生成更大的数。
2. 特性差异
因数的特性:因数的数量有限(对于非零自然数而言),且每个因数都小于或等于被除数。特别地,1和该数本身总是其因数,这被称为因数的平凡性。同时,因数的存在也体现了数的可分性,即一个数可以被拆解为更小、更基本的部分。
倍数的特性:倍数的数量是无穷的,且每个倍数都大于或等于给定的数(除非该数为0,但通常在数学讨论中排除0作为倍数的起点)。倍数展示了数的增长性和扩展性,通过简单的乘法运算,我们可以得到一个数的所有可能倍数。
3. 相互关系
尽管因数和倍数在定义和特性上存在明显区别,但它们之间也存在着紧密的联系。任何非零自然数的因数集和倍数集共同构成了该数在数轴上的“邻域”,反映了数与数之间的基本关系。更重要的是,通过寻找一个数的所有因数,我们可以间接地了解到它的质因数分解,这是理解数论和代数结构的重要工具。而倍数的计算,则有助于我们理解数的扩展性和周期性,在解决实际问题时提供便利。
三、实践应用:深化理解,提升能力
为了更有效地掌握因数和倍数的概念,并将其应用于实际问题中,我们可以尝试以下几种方法:
1. 动手操作:利用实物或图形,如积木、卡片等,进行因数和倍数的直观演示。例如,通过组合不同数量的积木来表示一个数的不同因数,或者排列相同数量的积木来展示倍数关系。
2. 列表比较:针对特定的数,列出其所有因数和部分倍数,通过对比列表来直观感受两者的差异。同时,可以观察并分析不同数之间因数和倍数的变化规律。
3. 解决问题:将因数和倍数的知识融入实际问题中,如购物时计算商品的总价(倍数的应用)、分配物品时确保每份均等(因数的应用)等。通过解决实际问题,不仅能够巩固理论知识,还能提升数学应用能力。
4. 归纳总结:在学习过程中,及时归纳总结因数和倍数的性质、特点及应用场景,形成系统的知识体系。这样不仅有助于记忆和理解,还能为后续学习打下坚实的基础。
总之,因数和倍数是数学中的基础而重要的概念。通过深入理解其定义、特性及相互关系,结合实践操作和问题解决,我们能够有效地区分这两个概念,并在数学学习中获得更大的收获。希望本文的探讨能为读者点亮一盏明灯,照亮探索数学奥秘的道路。
-
 身份证正反面识别与区分资讯攻略10-29
身份证正反面识别与区分资讯攻略10-29 -
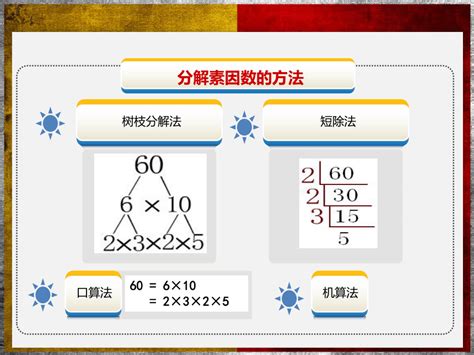 探索因数分解的奇妙方法资讯攻略12-06
探索因数分解的奇妙方法资讯攻略12-06 -
 如何区分习惯思维、思维定势与功能固着:三者的关键差异在哪里?资讯攻略11-04
如何区分习惯思维、思维定势与功能固着:三者的关键差异在哪里?资讯攻略11-04 -
 如何正确区分左右手?资讯攻略11-06
如何正确区分左右手?资讯攻略11-06 -
 如何明确区分古奇(Gucci)与古驰(品牌误区解析)资讯攻略10-24
如何明确区分古奇(Gucci)与古驰(品牌误区解析)资讯攻略10-24 -
 冷冻与冷藏:一文带你轻松区分两者差异资讯攻略10-25
冷冻与冷藏:一文带你轻松区分两者差异资讯攻略10-25












