探索因数分解的奇妙方法

分解因数怎么分：一步步带你理解

在数学学习中，分解因数是一个非常重要且基础的概念。无论你是小学生还是中学生，甚至在数学研究或日常应用中，分解因数都是一个频繁出现的工具。那么，分解因数究竟是什么呢？怎么分解因数呢？本文将从多个角度，用通俗易懂的语言，详细介绍分解因数的方方面面。

一、什么是分解因数

首先，我们要明白什么是因数。因数就是能够整除一个数的整数，比如1、2、3、4都是12的因数，因为它们都能整除12，没有余数。分解因数，简单来说，就是把一个数分解成几个因数的乘积。

举个例子，12可以分解为3和4的乘积，也可以分解为2和6的乘积，甚至还可以分解为1、2和6三个因数的乘积（注意，这里我们通常考虑的是质因数分解以外的所有可能组合）。但最常用的还是质因数分解，即把一个数分解为若干个质数相乘的形式。质数是只有1和它本身两个正因数的自然数，如2、3、5、7等。

二、为什么要分解因数

你可能会问，为什么要学习分解因数呢？它在实际生活中有什么用呢？其实，分解因数在数学和实际应用中都有着广泛的应用。

1. 简化计算：通过分解因数，我们可以简化一些复杂的计算。比如，计算两个数的最大公约数（GCD）和最小公倍数（LCM）时，利用分解因数的方法会更加直观和高效。

2. 问题解决：很多数学问题都涉及到分解因数。比如，密码学中的一些算法就利用了因数分解的难度来实现加密。

3. 实际应用：在物理学、化学、工程学等领域，分解因数也有广泛的应用。比如，在信号处理中，对信号进行频域分解，本质上也是一种因数分解的过程。

三、如何分解因数

接下来，我们重点介绍如何分解因数，特别是如何进行质因数分解。

1. 试除法

试除法是最直观的一种方法。我们从最小的质数2开始，尝试用它去除给定的数。如果能整除，那么这个数就是给定数的一个因数，我们继续用2去除商，直到商不能再被2整除为止。然后，我们再用下一个质数3去除这个商，以此类推，直到商为1为止。

例如，分解28的质因数：

28 ÷ 2 = 14（2是因数）

14 ÷ 2 = 7（2又是因数，商为7）

7不能再被2整除，我们尝试下一个质数3，但7 ÷ 3有余数，所以3不是因数。

7也不能被5整除（因为5大于7的平方根，且7不是5的倍数），所以我们可以确定7是一个质因数。

因此，28的质因数分解为2 × 2 × 7。

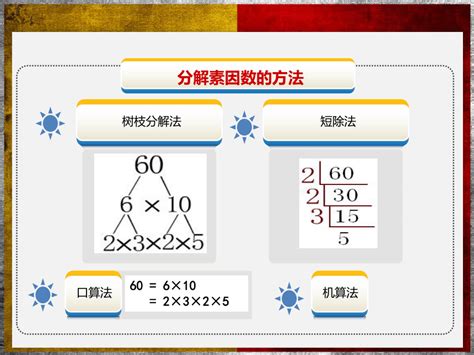
2. 分解质因数树

为了更直观地展示分解过程，我们可以使用分解质因数树。这种方法特别适合小学生，因为它非常直观，易于理解。

例如，分解36的质因数：

从36开始，找到最小的质因数2，画出一个分支，写上2和18（36 ÷ 2 = 18）。

对18继续分解，找到最小的质因数2，再画出一个分支，写上2和9（18 ÷ 2 = 9）。

对9进行分解，发现它只能被3整除，因此写下3和3（9 ÷ 3 = 3）。

最后，3是一个质数，不能再分解。

将这个过程画成树状图，就可以清晰地看到36的质因数分解为2 × 2 × 3 × 3。

3. 特殊情况的处理

完全平方数：如果一个数是完全平方数（如36=6²），那么在分解质因数时，会有一个质因数出现两次。

奇数：除了2以外的质数都是奇数，因此当我们在分解一个奇数时，可以跳过偶数质因数2。

偶数：任何偶数都可以被2整除，因此，在分解偶数时，我们可以先不断地除以2，直到商为奇数为止，然后再按奇数的方法分解。

四、分解因数的注意事项

在分解因数时，有几个注意事项需要牢记：

1. 检查完整性：确保你分解出来的因数乘积等于原数。比如，如果你分解出来的因数是2、3和5，那么它们的乘积应该是30，如果原数是30，那么分解就是正确的。

2. 唯一性：除了排列顺序外，一个数的质因数分解是唯一的。也就是说，不同的分解方式最终会得到相同的质因数组合。

3. 不重复：在分解过程中，避免重复使用同一个质因数。比如，在分解36时，我们不会写两次2（即2 × 2 × 2 × 9），因为这样会重复计算。

4. 使用工具：对于较大的数，手动分解可能比较困难，可以使用计算器或编程软件来辅助。

五、总结

分解因数是一个既基础又重要的数学概念，它可以帮助我们简化计算、解决数学问题，并在实际生活中找到广泛的应用。通过试除法、分解质因数树等方法，我们可以轻松地分解一个数的因数。在分解过程中，要注意完整性、唯一性、不重复性和工具的使用。

希望这篇文章能帮助你更好地理解和掌握分解因数的技巧，让你在数学学习和实际应用中更加得心应手。无论是小学生还是中学生，甚至是成年人，都可以通过分解因数这一工具，探索数学的奥秘，享受数学带来的乐趣。