分数乘以整数的计算方法

在数学学习中，分数乘整数是一个基础且重要的知识点。它不仅在日常生活中有着广泛的应用，还是进一步学习更复杂数学概念的基础。本文将从定义、计算方法、步骤、实例以及注意事项等多个方面，详细介绍分数乘整数的计算方法，旨在帮助读者掌握这一基本技能。

首先，我们需要明确什么是分数和整数。分数是表示一个整体被平均分成若干等份后，取其中几份的数。它由分子、分母和分数线组成，例如1/2、3/4等。整数则包括正整数、零和负整数，如1、-3、0等。

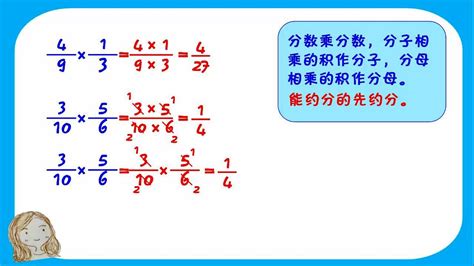
分数乘整数的定义

分数乘整数，指的是将一个分数与一个整数相乘，结果是一个新的分数或整数。这个计算过程遵循数学中的乘法分配律，即整数与分数的每一个部分（分子）相乘，然后再将结果与分母相结合。

计算方法

分数乘整数的计算方法相对简单，可以概括为以下几个步骤：

1. 确定乘法对象：明确题目中给出的分数和整数。

2. 整数与分子相乘：将整数与分数的分子相乘，得到一个新的乘积。

3. 保持分母不变：分数的分母在乘法过程中保持不变。

4. 简化结果（如有必要）：如果得到的结果是一个分数，且分子和分母有公约数，则进行约分，得到最简分数。

具体步骤与实例

为了更好地理解分数乘整数的计算方法，我们可以通过以下实例进行说明：

实例一：2 × 3/4

1. 确定乘法对象：整数2和分数3/4。

2. 整数与分子相乘：2 × 3 = 6。

3. 保持分母不变：分母4保持不变。

4. 组合结果：得到新的分数6/4。

5. 简化结果：6和4有公约数2，进行约分，得到最简分数3/2，也可以转化为带分数1又1/2。

实例二：-5 × 2/7

1. 确定乘法对象：整数-5和分数2/7。

2. 整数与分子相乘：-5 × 2 = -10。

3. 保持分母不变：分母7保持不变。

4. 组合结果：得到新的分数-10/7。

5. 无需简化：因为-10和7没有公约数，所以-10/7已经是最简形式。

实例三：0 × 5/6

1. 确定乘法对象：整数0和分数5/6。

2. 整数与分子相乘：0 × 5 = 0。

3. 保持分母不变：分母6保持不变（但实际上这一步在此例中并无实际意义，因为整数为0时，结果必然为0）。

4. 组合结果：得到0。

注意事项

在进行分数乘整数的计算时，需要注意以下几点：

1. 符号处理：当整数为负数时，要确保将负号传递给结果的分子。

2. 约分：在计算过程中，如果得到的分数可以约分，则务必进行约分，以得到最简结果。

3. 零的特殊性：任何数与0相乘都等于0，这一规则同样适用于分数乘整数。

4. 分数与整数的互化：在某些情况下，为了方便计算或表达，可能需要将分数转化为整数（如通过乘除法的逆运算），或将整数看作分母为1的分数。

分数乘整数的应用

分数乘整数在日常生活和工作中有着广泛的应用。例如：

烹饪：在烘焙或烹饪时，经常需要根据食谱中的比例调整食材的数量。这时，分数乘整数就显得尤为重要。

工程：在建筑工程或机械设计中，经常需要计算材料的用量或尺寸的比例。分数乘整数能够帮助工程师快速准确地完成这些计算。

金融：在财务计算中，如计算利息、折扣或比例分配时，分数乘整数也是必不可少的工具。

科学：在物理学、化学等科学领域，分数乘整数被广泛应用于计算质量、体积、速度等物理量的比例关系。

提高计算效率的技巧

为了提高分数乘整数的计算效率，可以掌握以下技巧：

1. 熟记常见分数与整数的乘积：通过反复练习，熟记一些常见分数（如1/2、1/3、1/4等）与整数的乘积，可以大大提高计算速度。

2. 利用乘法分配律：在处理复杂的分数乘法时，可以利用乘法分配律将问题拆