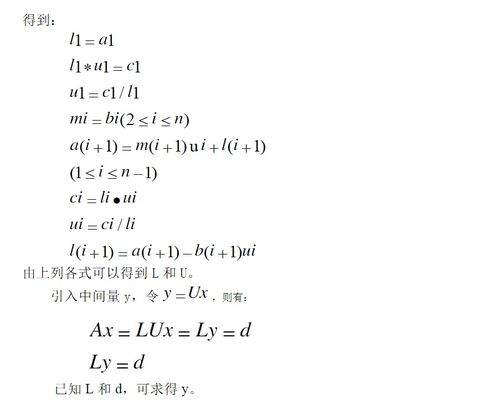揭秘波动现象的奥秘：深入探索波动方程的三种核心表达式

波动方程的三种表达式

波动方程是描述波动现象的重要数学工具，它描述了波动在空间和时间中的传播特性。波动方程有多种表达式，每种表达式都适用于不同的物理背景和情境。本文将详细介绍波动方程的三种主要表达式：一维波动方程、三维波动方程以及波动方程的矢量形式。

一、一维波动方程

一维波动方程是最基本也是最简单的波动方程形式，它通常用于描述在一维空间中传播的波动，如弦上的波动或声波在管道中的传播。一维波动方程的一般形式可以表示为：

\[ \frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^2 u}{\partial x^2} \]

其中，\(u(x, t)\) 表示波动在位置 \(x\) 和时间 \(t\) 的位移或振幅，\(c\) 是波速，表示波动传播的速度。

这个方程的物理意义在于，它描述了波动在时间上的二阶导数与在空间上的二阶导数之间的关系。换句话说，它揭示了波动在时间上的加速度与在空间上的曲率之间的关系。这种关系正是波动传播的基础。

为了更直观地理解这个方程，我们可以考虑一个具体的物理情境：一根紧绷的弦在受到外力作用后产生的波动。在这个情境中，弦上的每一点都会随时间做周期性的振动，而这种振动会沿着弦传播出去。一维波动方程正是描述了这种振动传播的数学规律。

二、三维波动方程

与一维波动方程相比，三维波动方程更为复杂，但它描述了波动在三维空间中的传播特性，因此具有更广泛的应用。三维波动方程的一般形式可以表示为：

\[ \frac{\partial^2 u}{\partial t^2} = c^2 \left( \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2} \right) \]

这个方程的形式与一维波动方程类似，但包含了三个空间坐标 \(x\)、\(y\) 和 \(z\)，因此描述了波动在三维空间中的传播。同样地，\(u(x, y, z, t)\) 表示波动在位置 \((x, y, z)\) 和时间 \(t\) 的位移或振幅，\(c\) 是波速。

三维波动方程在物理学和工程学中有广泛的应用。例如，在地震学中，它用于描述地震波在地球内部的传播；在声学中，它用于描述声波在空气中的传播；在电磁学中，它用于描述电磁波在空间中的传播。

为了求解三维波动方程，通常需要采用数值方法或近似方法，因为直接求解这个方程往往非常复杂。然而，在一些特殊情况下，如波动在均匀介质中传播且边界条件简单时，我们可以找到这个方程的精确解。

三、波动方程的矢量形式

除了上述的一维和三维波动方程外，还有一种更为通用的波动方程形式，即波动方程的矢量形式。这种形式适用于描述在复杂介质中传播的波动，如弹性介质中的声波或电磁波在不均匀介质中的传播。

波动方程的矢量形式可以表示为：

\[ \nabla^2 \mathbf{u} - \frac{1}{c^2} \frac{\partial^2 \mathbf{u}}{\partial t^2} = 0 \]

其中，\(\mathbf{u}(\mathbf{r}, t)\) 表示波动在位置 \(\mathbf{r}\) 和时间 \(t\) 的位移或振幅矢量，\(\nabla^2\) 是拉普拉斯算子，表示空间中的二阶导数，\(c\) 是波速。

这个方程的形式比一维和三维波动方程更为抽象，但它具有更强的通用性。它可以描述各种不同类型的波动，包括标量波（如声波）和矢量波（如电磁波）。此外，它还适用于描述在复杂介质中传播的波动，如非线性介质或具有色散效应的介质。

在求解波动方程的矢量形式时，通常需要采用更为复杂的数学工具和方法，如矢量分析、偏微分方程理论和数值方法等。然而，这种形式的波动方程为我们提供了一种更为统一和通用的描述波动的方法，使我们能够更好地理解和预测波动在各种介质中的传播特性。

总结

波动方程是描述波动现象的重要数学工具，它有多种表达式，每种表达式都适用于不同的物理背景和情境。一维波动方程是最基本的形式，用于描述在一维空间中传播的波动；三维波动方程则描述了波动在三维空间中的传播特性；而波动方程的矢量形式则具有更强的通用性，适用于描述在复杂介质中传播的波动。

通过学习和理解波动方程的三种主要表达式，我们可以更好地把握波动现象的本质和规律，为相关领域的研究和应用提供有力的数学支持。同时，我们也应该注意到，波动方程的求解往往比较复杂，需要采用适当的数学工具和方法进行求解和分析。因此，在实际应用中，我们需要根据具体的问题背景和需求选择合适的波动