二进制转八进制轻松教程
二进制和八进制是计算机科学中非常重要的数制,尤其在底层编程和系统设计中,它们扮演着至关重要的角色。二进制只有0和1两种状态,非常适合计算机内部的逻辑运算,而八进制则因为每一位数字可以表示三个二进制位(bit),所以在阅读和书写上比二进制更为方便。那么,如何将二进制转换成八进制呢?本文将详细介绍一种简单且实用的方法,让你轻松掌握这一技能。

首先,我们需要理解二进制和八进制的基本概念。二进制,顾名思义,就是基于二的数制,它只有两个数字:0和1。在计算机内部,所有的信息都是以二进制的形式存储和处理的。而八进制,则是基于八的数制,它有八个数字:0、1、2、3、4、5、6和7。八进制的一个显著优点是,每一位数字可以对应二进制中的三位,这使得在表示较大的二进制数时,八进制更为简洁。
接下来,我们来看具体的转换步骤。假设我们有一个二进制数,想要将其转换为八进制,可以按照以下步骤进行:
第一步,将二进制数从右向左每三位一组进行划分。如果二进制数的位数不是三的倍数,那么在最左边的一组中,不足三位的部分用0补齐。这一步的目的是为了将二进制数按照八进制每一位对应的二进制位数进行分组,便于后续的转换。
例如,我们有一个二进制数:110101101。按照每三位一组进行划分,得到:001 101 011 01(注意,最左边的一组我们用0补齐了两位,使其成为一个三位数)。
第二步,将每一组三位二进制数转换为对应的八进制数。这一步需要用到二进制到十进制的转换规则,但因为我们是在转换到八进制,所以实际上我们是在找每一位二进制数在八进制中的对应值。
对于每一组三位二进制数,我们可以将其看作是一个二进制表示的十进制数,然后找出这个十进制数在八进制中的对应值。例如,对于二进制数001,它表示的十进制数是1,而1在八进制中仍然是1;对于二进制数101,它表示的十进制数是5,5在八进制中也是5;对于二进制数011,它表示的十进制数是3,3在八进制中还是3;最后,对于二进制数010,它表示的十进制数是2,2在八进制中也是2(注意,这里我们实际上没有用到010这一组,因为我们在第一步中补齐了位数,但理解这个过程对于掌握转换方法是有帮助的)。
然而,在实际操作中,我们并不需要真的将每一组三位二进制数转换为十进制数,然后再找出这个十进制数在八进制中的对应值。我们可以直接利用二进制到八进制的映射关系进行转换。这个映射关系是这样的:
000 -> 0
001 -> 1
010 -> 2
011 -> 3
100 -> 4
101 -> 5
110 -> 6
111 -> 7
有了这个映射关系,我们就可以直接将每一组三位二进制数转换为对应的八进制数了。例如,对于二进制数001,它直接对应八进制数1;对于二进制数101,它直接对应八进制数5;以此类推。
所以,对于我们的二进制数110101101,按照每三位一组进行划分并转换后,得到的八进制数是:1535(注意,这里我们省略了最左边补齐的0,因为它们不影响最终的转换结果)。
第三步,将转换得到的八进制数按照从高位到低位的顺序排列起来,就是我们最终的答案。
在我们的例子中,最终的八进制数是1535。
此外,还有一些特殊情况需要注意。如果二进制数的位数正好是三的倍数,那么转换过程就会非常顺利。但如果二进制数的位数不是三的倍数,那么在最左边的一组中,我们需要用0补齐位数。这些补齐的0在八进制表示中是不会显示出来的,但它们确实参与了转换过程。
另外,如果二进制数中包含连续的0(即不是每一位都是1或0交替出现),那么在转换过程中,这些0也会按照上述方法被正确地转换为八进制数中的0。例如,二进制数1000000会被转换为八进制数100(注意,这里的000000是被当作一个整体进行转换的,它对应八进制数中的00,但八进制表示中通常省略掉前导的0)。
总的来说,将二进制数转换为八进制数的过程并不复杂。只要理解了二进制和八进制的基本概念,掌握了每三位二进制数对应一位八进制数的转换规则,以及如何处理位数不是三的倍数的情况,就可以轻松地进行转换了。
通过本文的介绍,相信你已经掌握了将二进制数转换为八进制数的方法。在实际应用中,这一技能可以帮助你更好地理解计算机内部的数据存储和处理方式
- 上一篇: 如何正确填写政治面貌,一看就懂!
- 下一篇: 南瓜的18种家常做法及窍门,你知道吗?
-
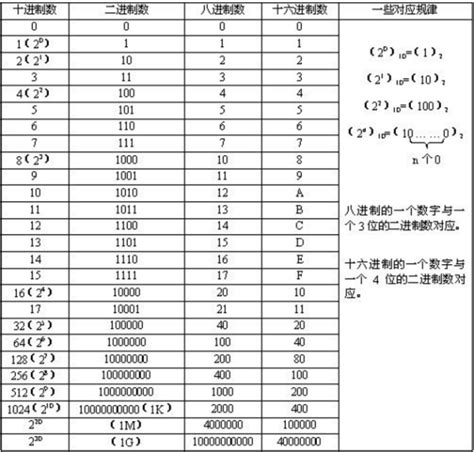 轻松掌握:16进制转10进制的方法资讯攻略12-03
轻松掌握:16进制转10进制的方法资讯攻略12-03 -
 十进制转二进制,轻松学会!资讯攻略10-29
十进制转二进制,轻松学会!资讯攻略10-29 -
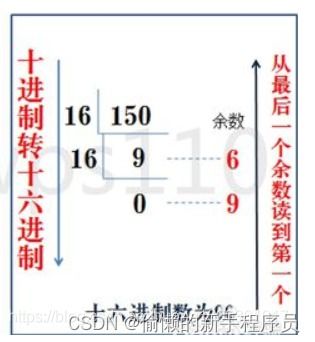 轻松学会:16进制转10进制的方法资讯攻略11-23
轻松学会:16进制转10进制的方法资讯攻略11-23 -
 二进制转十进制与十进制转二进制的方法是什么?资讯攻略10-24
二进制转十进制与十进制转二进制的方法是什么?资讯攻略10-24 -
 二进制转十进制的方法资讯攻略11-10
二进制转十进制的方法资讯攻略11-10 -
 十六进制转二进制的详细方法资讯攻略11-07
十六进制转二进制的详细方法资讯攻略11-07