十进制转二进制，轻松学会！

在我们日常生活的数字世界里，十进制（也就是我们通常所说的“普通数制”，如1、2、3...）是最常见的计数方式。然而，在计算机科学中，二进制（由0和1组成的数制）才是主角。这是因为计算机内部的所有运算和存储，都是基于二进制进行的。那么，十进制是如何转化为二进制的呢？本文将详细介绍这一过程，让即使是没有计算机背景的朋友也能轻松理解。

一、认识二进制

首先，让我们简单了解一下二进制。二进制是一种只有0和1两种符号的数制，它是计算机内部信息表示的基础。在计算机科学中，所有的数据，无论是文字、图像还是声音，最终都会被转化为二进制形式进行处理和存储。

二、十进制与二进制的关系

十进制是我们日常生活中最熟悉的数制，每一位数字的取值范围是0-9，满十进一。而二进制则是每一位只能取0或1，满二进一。那么，十进制数是如何转化为二进制数的呢？

三、十进制转化为二进制的方法

1. 反复除2取余法

这是最常用的十进制转化为二进制的方法。具体步骤如下：

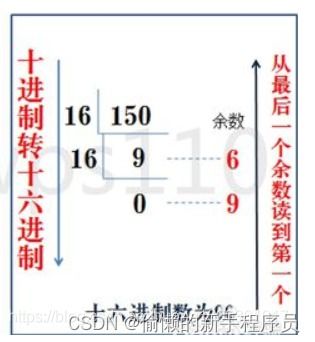
步骤一：将十进制数除以2，记录下余数。

步骤二：将得到的商再次除以2，再次记录下余数。

步骤三：重复上述步骤，直到商为0为止。

步骤四：将记录下的所有余数按照倒序排列，得到的数就是该十进制数的二进制表示。

例如，我们要将十进制数23转化为二进制数：

23 ÷ 2 = 11 余 1

11 ÷ 2 = 5 余 1

5 ÷ 2 = 2 余 1

2 ÷ 2 = 1 余 0

1 ÷ 2 = 0 余 1

将得到的余数倒序排列，得到10111，所以十进制数23的二进制表示是10111。

2. 基数乘除法

这种方法相对复杂一些，但在某些情况下也很有用。具体步骤如下：

步骤一：将十进制数除以2的幂次方（从最高次幂开始），直到商为0或小于2的幂次方为止。

步骤二：记录下每一步得到的商和余数。

步骤三：根据得到的商和余数，构造出二进制数。如果某一步的商为0，则在该位上写0；如果余数为1，则在该位上写1。

例如，我们还是将十进制数23转化为二进制数：

23 ÷ 2^4 = 1 余 7（2^4=16，因为23大于16）

7 ÷ 2^3 = 0 余 7（2^3=8，因为7小于8）

接下来，我们不再考虑2^3的商，而是将7继续除以更低的幂次方，但在这个例子中，7已经是小于8的数，所以我们直接考虑它的二进制表示。

7可以表示为111（二进制），因为7 = 4 + 2 + 1 = 2^2 + 2^1 + 2^0 = 111（二进制）。

但是，这种方法在实际操作中比较复杂，我们更常用的是反复除2取余法。

四、十进制小数转化为二进制

除了整数部分，十进制的小数部分也可以转化为二进制。具体方法如下：

步骤一：将十进制小数乘以2，记录下结果的整数部分（0或1）。

步骤二：将上一步得到的小数部分再次乘以2，再次记录下结果的整数部分。

步骤三：重复上述步骤，直到小数部分为0或达到所需的精度为止。

步骤四：将记录下的所有整数部分按照顺序排列（从左到右），得到的数就是该十进制小数的二进制表示（小数部分）。

例如，我们要将十进制小数0.375转化为二进制小数：

0.375 × 2 = 0.75，整数部分为0

0.75 × 2 = 1.5，整数部分为1

0.5 × 2 = 1，整数部分为1

将得到的整数部分按照顺序排列，得到0.011，所以十进制小数0.375的二进制表示是0.011。

五、注意事项

精度问题：在将十进制小数转化为二进制时，由于二进制无法精确表示某些十进制小数（如0.1），因此可能会得到一个无限循环的二进制小数。在实际应用中，我们通常会根据需要的精度来截取一定位数的小数部分。