抛物线相关公式全面总结
在数学的浩瀚宇宙中,抛物线如同一道优雅的弧线,连接着几何与代数的奇妙世界。它不仅是高中数学的重点内容,也是物理、工程等多个领域不可或缺的工具。想要深入探索这一美妙的数学形态,掌握其所有公式无疑是关键一步。今天,就让我们一起揭开抛物线的神秘面纱,汇总那些让你在解题中如虎添翼的公式,让数学之旅更加顺畅。

一、抛物线的基础定义与标准方程
首先,让我们从抛物线的基础定义出发。抛物线是指平面上与一固定点(焦点)和一条直线(准线)等距的点的轨迹。这一简洁而深刻的定义,为我们打开了通往抛物线奥秘的大门。

根据抛物线的开口方向和轴线的位置,其标准方程可以分为四种形式:

1. 开口向右或向左的抛物线:\(y = ax^2 + bx + c\)(当\(a>0\)时开口向上,\(a<0\)时开口向下)。通过配方,可转化为顶点式\(y = a(x - h)^2 + k\),其中\((h, k)\)为顶点坐标。

2. 开口向上或向下的抛物线:\(x = ay^2 + by + c\),同样可转化为顶点式\(x = a(y - k)^2 + h\)。
3. 顶点式:\(y = a(x - h)^2 + k\) 或 \(x = a(y - k)^2 + h\),直接给出了抛物线的顶点坐标和开口方向。
4. 参数式:在某些情况下,使用参数方程描述抛物线更为方便,如\(x = t + at^2\),\(y = bt + ct^2\),其中\(t\)为参数。
二、抛物线的焦点、准线及性质
抛物线的焦点和准线是理解其性质的关键。对于开口向右或向左的抛物线\(y = ax^2 + bx + c\),其焦点坐标为\(\left(\frac{-b}{2a}, c - \frac{b^2 - 4ac}{4a}\right)\)(或简化为\(\left(-\frac{b}{2a}, -\frac{\Delta}{4a}\right)\)),准线方程为\(y = c + \frac{1}{4a}\)(注意这里的\(\Delta = b^2 - 4ac\)为判别式)。对于开口向上或向下的抛物线,只需将\(x\)与\(y\)互换即可得到相应的焦点和准线方程。
此外,抛物线还具有一系列重要的性质:
对称性:抛物线关于其对称轴对称。
切线性质:抛物线上任一点的切线斜率与该点至焦点的连线斜率互为负倒数。
光学性质:平行于抛物线对称轴的光线经抛物线反射后,将聚焦于焦点;反之,从焦点发出的光线经抛物线反射后,将平行于对称轴。
三、抛物线的几何应用与公式推导
抛物线的应用广泛,不仅限于数学题目,更深入到物理和工程领域。在几何问题中,抛物线的性质常被用来解决最值问题、距离问题等。
求最值:利用顶点式,可以迅速找到抛物线的最大值或最小值。
求距离:如求点到抛物线的最短距离,常需结合抛物线的方程和点到直线的距离公式进行求解。
交点问题:求抛物线与直线或其他曲线的交点,需联立方程求解。
在推导相关公式时,如抛物线的弦长公式、切线方程等,往往需要灵活运用代数恒等式、导数等数学工具。例如,求抛物线\(y = ax^2 + bx + c\)上两点\(A(x_1, y_1)\)和\(B(x_2, y_2)\)之间的弦长,可先求出斜率\(k_{AB} = \frac{y_2 - y_1}{x_2 - x_1}\),再利用两点间距离公式\(\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\),结合抛物线方程进行化简。
四、抛物线与物理的联系
在物理学中,抛物线的应用同样广泛。最著名的莫过于经典力学中的抛体运动,物体在只受重力作用下的运动轨迹即为抛物线(忽略空气阻力)。此时,物体的水平位移\(x\)、竖直位移\(y\)、时间\(t\)之间的关系,可以通过解抛体运动的方程组得到,其解往往呈现为抛物线的形式。
此外,在光学、声学等领域,抛物线的聚焦性质也被广泛应用。如抛物面反射镜,能将平行光线聚焦于一点,这一原理被广泛应用于天文望远镜、探照灯等设备中。
五、抛物线的高级概念与公式
-
 揭秘:顶点公式的详细解析资讯攻略11-22
揭秘:顶点公式的详细解析资讯攻略11-22 -
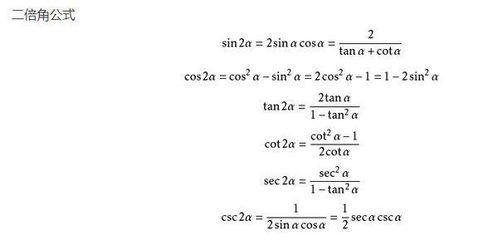 精通常见三角函数积分:公式推导与全面总结资讯攻略11-18
精通常见三角函数积分:公式推导与全面总结资讯攻略11-18 -
 打造精彩年度总结:全面指南资讯攻略11-23
打造精彩年度总结:全面指南资讯攻略11-23 -
 含水量计算公式详解资讯攻略11-15
含水量计算公式详解资讯攻略11-15 -
 如何撰写个人年度总结?资讯攻略11-27
如何撰写个人年度总结?资讯攻略11-27 -
 如何高效撰写销售总结,提升业绩反思效果资讯攻略11-27
如何高效撰写销售总结,提升业绩反思效果资讯攻略11-27