精通常见三角函数积分：公式推导与全面总结

三角函数在微积分学中占有重要地位，尤其在积分计算中，常见三角函数如正弦、余弦、正切等的积分公式是基础且频繁使用的工具。本文旨在推导与总结这些基本三角函数的积分公式，以便读者能够深入理解并掌握这些公式的应用。

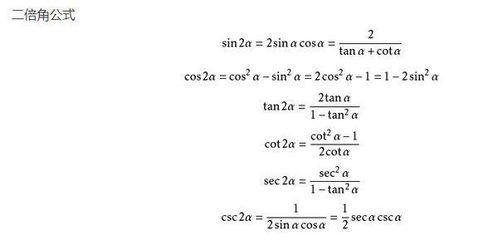
引入与预备知识

在正式推导之前，我们先回顾一下基本的积分法则和三角函数的基本性质。积分是微分的逆运算，用于计算函数在某区间上的累积效果。而三角函数，如正弦sin(x)、余弦cos(x)、正切tan(x)等，在周期性函数和波动现象的描述中至关重要。

基本积分法则

1. 常数积分：∫k dx = kx + C，其中k是常数，C是积分常数。

2. 幂函数积分：∫x^n dx = (1/(n+1))x^(n+1) + C，n ≠ -1。

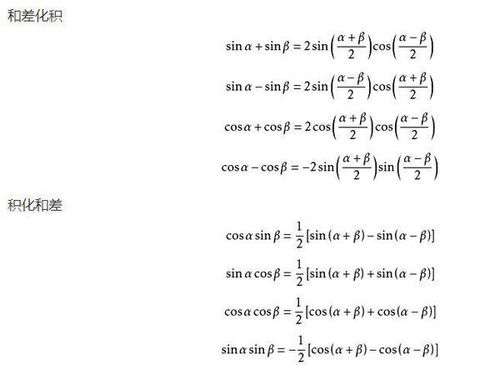
3. 和差积分：∫(f(x) + g(x)) dx = ∫f(x) dx + ∫g(x) dx。

4. 换元积分：通过变量替换简化积分过程。

5. 分部积分：∫u dv = uv - ∫v du，适用于乘积形式的函数积分。

正弦函数的积分

对于正弦函数sin(x)的积分，我们利用基本积分法则和三角函数的基本恒等式来推导。

推导过程：

设 ∫sin(x) dx = -cos(x) + C，其中C为积分常数。

验证：

对 -cos(x) + C 求导，得到 d/(-dx) (-cos(x) + C) = sin(x)。

由于导数等于原函数，故该积分公式正确。

余弦函数的积分

余弦函数cos(x)的积分与正弦函数类似，同样利用基本积分法则和三角函数的基本恒等式。

推导过程：

设 ∫cos(x) dx = sin(x) + C，其中C为积分常数。

验证：

对 sin(x) + C 求导，得到 d/dx (sin(x) + C) = cos(x)。

导数等于原函数，故该积分公式正确。

正切函数的积分

正切函数tan(x)的积分稍显复杂，因为它涉及到对数函数。我们利用正切的定义和换元积分法来推导。

推导过程：

首先，正切tan(x)可以表示为sin(x)/cos(x)。

设 ∫tan(x) dx = ∫(sin(x)/cos(x)) dx。

通过换元法，令u = cos(x)，则du = -sin(x)dx。

所以，∫(sin(x)/cos(x)) dx = -∫(1/u) du = -ln|u| + C = -ln|cos(x)| + C。

验证：

对 -ln|cos(x)| + C 求导，得到 d/dx (-ln|cos(x)| + C) = tan(x)。

导数等于原函数，故该积分公式正确。

余切函数的积分

余切函数cot(x)的积分与正切函数类似，也涉及到对数函数。我们利用余切的定义和换元积分法来推导。

推导过程：

首先，余切cot(x)可以表示为cos(x)/sin(x)。

设 ∫cot(x) dx = ∫(cos(x)/sin(x)) dx。

通过换元法，令u = sin(x)，则du = cos(x)dx。

所以，∫(cos(x)/sin(x)) dx = ∫(1/u) du = ln|u| + C = ln|sin(x)| + C。

验证：

对 ln|sin(x)| + C 求导，得到 d/dx (ln|sin(x)| + C) = cot(x)。

导数等于原函数，故该积分公式正确。

三角函数的复合积分

除了基本三角函数外，我们还会遇到它们的复合形式，如sin^2(x)、cos^2(x)等。这些积分通常通过三角恒等式或换元法来解决。

sin^2(x)的积分：

利用三角恒等式sin^2(x) = (1 - cos(2x))/2，得到：

∫sin^2(x) dx = ∫(1 - cos(2x))/2 dx = (1/2)∫dx - (1/2)∫cos(2x) dx = x/2 - (1/4)sin(2x) + C。

cos^2(x)的积分：

利用三角恒等式cos^2(x) = (1 + cos(2x))/2，得到：

∫cos^2(x) dx = ∫(1 + cos(2x))/2 dx = (1/2)∫dx + (1/2)∫cos(2x) dx = x/2 + (1/4)sin(2x) + C。

总结

通过上述推导，我们得到了常见三角函数的基本积分公式：

∫sin(x) dx = -cos(x) + C

∫cos(x) dx = sin(x) + C

∫tan(x) dx = -ln|cos(x)| + C

∫cot(x) dx = ln|sin(x)| + C

∫sin^2(x) dx = x/2 - (1/4)sin(2x) + C

∫cos^2(x) dx = x/2 + (1/4)sin(2x) + C

这些公式在积分计算中非常实用，尤其在处理涉及三角函数的物理问题和工程问题时。掌握这些公式及其推导过程，不仅有助于理解三角函数的性质，还能提高解决复杂积分问题的能力。

应用与拓展

在实际应用中，这些积分公式经常用于求解微分方程、计算面积、体积以及物理现象的定量分析。此外，随着学习的深入，我们还将遇到更多复杂的三角函数积分，如包含三角函数的乘积、复合函数以及反三角函数的积分。这时，掌握基本的积分技巧和方法，如换元法、分部积分法、三角恒等式的应用等，将显得尤为重要。

通过不断练习和实践，我们可以逐渐熟悉这些公式的应用，提高解决复杂问题的能力。同时，了解三角函数的积分在各个领域中的实际应用，也能激发我们的学习兴趣，使我们在数学学习和实践中取得更好的成绩。