三角形边长关系公式详解
在几何学中,三角形作为最基本的多边形之一,其性质和公式在日常生活、工程设计以及科学研究中有着广泛的应用。其中,三角形的边长公式是理解三角形特性的基础,它不仅能够帮助我们计算三角形的边长,还能进一步推导出三角形的面积、角度等其他重要属性。本文将从三角形的定义与分类、边长公式的推导、海伦公式及其应用、余弦定理及其扩展,以及边长公式在实际问题中的应用等多个维度,深入探讨三角形的边长公式。

三角形的定义与分类
三角形是由三条直线(或线段)首尾相连围成的封闭图形。这三条直线被称为三角形的边,而它们之间的夹角则被称为三角形的角。根据边长和角度的不同,三角形可以分为以下几类:
1. 等边三角形:三边等长,三个角均为60度。
2. 等腰三角形:有两边等长,对应的两个角相等。
3. 不等边三角形:三边长度各不相同,三个角也各不相同。
4. 直角三角形:有一个角为90度,根据勾股定理,直角边的平方和等于斜边的平方。
边长公式的推导
对于不同类型的三角形,其边长公式的推导方式有所不同。
勾股定理
直角三角形是最容易推导边长公式的三角形类型。勾股定理(也称为毕达哥拉斯定理)指出,在一个直角三角形中,直角边的平方和等于斜边的平方,即:
\[a^2 + b^2 = c^2\]
其中,\(a\) 和 \(b\) 是直角三角形的两条直角边,\(c\) 是斜边。这个公式不仅适用于直角三角形,还可以作为其他类型三角形边长计算的基础,尤其是在解决涉及垂直高度或投影长度的问题时。
海伦公式
对于任意三角形,海伦公式提供了一种通过三边长度计算三角形面积的方法,但反过来,它也可以帮助我们理解边长之间的关系。海伦公式表述为:
\[S = \sqrt{p(p-a)(p-b)(p-c)}\]
其中,\(S\) 是三角形的面积,\(a\)、\(b\)、\(c\) 是三角形的三边长度,\(p\) 是半周长,即 \(\frac{a+b+c}{2}\)。虽然海伦公式直接用于计算面积,但通过分析面积与边长之间的关系,我们可以间接推导出边长之间的约束条件,尤其是在已知两边长度和夹角或已知三边长度求角度时。
余弦定理
余弦定理是处理非直角三角形边长和角度关系的重要工具。它表述为:
\[c^2 = a^2 + b^2 - 2ab\cos C\]
其中,\(a\)、\(b\)、\(c\) 是三角形的三边长度,\(C\) 是边 \(c\) 所对的角。余弦定理不仅可以直接用于求解未知边长,还可以结合正弦定理解决涉及角度的问题。
海伦公式及其应用
海伦公式虽然主要用于计算三角形的面积,但其背后的数学逻辑揭示了边长之间的深刻关系。通过海伦公式,我们可以推导出三角形边长必须满足的条件,即任意两边之和大于第三边,任意两边之差小于第三边。这一条件确保了三角形的存在性,也是三角形边长公式应用的基础。
在实际应用中,海伦公式常用于测量和工程领域,特别是在无法直接测量三角形高度或角度的情况下。例如,在土地测量中,通过测量三边的长度,可以利用海伦公式计算出土地的面积。
余弦定理及其扩展
余弦定理是处理三角形边长和角度关系的强大工具。它不仅适用于求解未知边长,还可以结合正弦定理解决更复杂的几何问题。正弦定理表述为:
\[\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R\]
其中,\(R\) 是三角形的外接圆半径。正弦定理和余弦定理的结合使用,可以解决几乎所有涉及三角形边长和角度的问题。
余弦定理的扩展形式还包括余弦的半角公式和余弦的和差公式,这些公式在解决更复杂的几何问题时非常有用。例如,在求解三角形的内角平分线长度、外心到顶点的距离等问题时,这些扩展形式能够提供额外的数学工具。
边长公式在实际问题中的应用
三角形的边长公式在日常生活和工程设计中有着广泛的应用。以下是一些具体的应用场景:
1. 建筑设计:在建筑设计中,三角形结构因其稳定性和强度而被广泛使用。通过精确计算三角形的边长,可以确保结构的稳定性和安全性。
2. 导航与定位:在导航系统中,三角形边长公式用于计算两点之间的距离和方位角,从而确定位置。例如,GPS系统就利用了三角形的边长和角度关系来确定接收器的精确位置。
3. 无线通信:在无线通信中,三角形的边长公式用于计算基站之间的信号覆盖范围,以及确定移动设备的位置。这有助于优化网络布局和提高通信质量。
4. 天文学:在天文学中,三角形边长公式用于计算天体之间的距离和相对位置。例如,通过观测恒星之间的角度和距离,可以绘制出星系的分布图。
5. 计算机图形学:在计算机图形学中,三角形是构成三维模型的基本单元。通过精确计算三角形的边长和角度,可以生成逼真的三维图像和动画效果。
综上所述,三角形的边长公式是几何学中的基础工具,它不仅帮助我们理解三角形的性质和结构,还在多个领域发挥着重要作用。通过深入学习和应用这些公式,我们可以更好地解决实际问题,推动科学技术的发展。
- 上一篇: 揭秘:降维打击的真正含义!
- 下一篇: 贴春联的讲究与规则:如何正确迎接新年春联
-
 等腰三角形边长计算公式详解资讯攻略10-29
等腰三角形边长计算公式详解资讯攻略10-29 -
 高中数学必备:全面三角函数公式集锦(终极版)资讯攻略12-01
高中数学必备:全面三角函数公式集锦(终极版)资讯攻略12-01 -
 等腰三角形面积如何计算?资讯攻略11-30
等腰三角形面积如何计算?资讯攻略11-30 -
 正方形周长计算公式详解资讯攻略10-31
正方形周长计算公式详解资讯攻略10-31 -
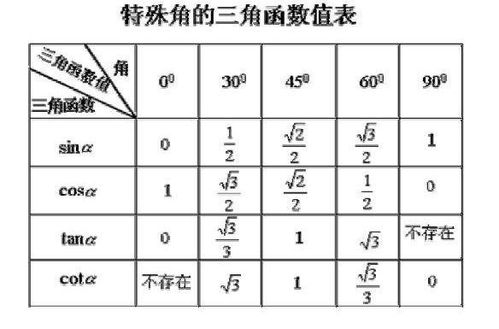 三角函数常见公式概览资讯攻略11-28
三角函数常见公式概览资讯攻略11-28 -
 含水量计算公式详解资讯攻略11-15
含水量计算公式详解资讯攻略11-15












