等腰三角形面积如何计算？

等腰三角形是几何学中一种重要的图形，它具有两边长度相等的特点，这使得在等腰三角形的面积计算中，可以利用其独特的性质简化计算过程。下面将详细介绍等腰三角形面积的计算方法，帮助读者全面理解和应用。

等腰三角形的基本定义是两边长度相等的三角形。假设等腰三角形的底边长为b，两条等边长为a，高为h。在已知等腰三角形的某些参数时，可以通过不同的方法计算其面积。

首先，最常见且最基础的方法是使用三角形面积的通用公式：面积 = (底 × 高) ÷ 2。在等腰三角形中，底是已知的，记为b，高可以通过不同的方法求得。

一种直接求高的方法是使用勾股定理。在等腰三角形中，若作底边的高，则高将底边分为两段相等的部分，每段长度为b/2。由于高、底边的一半和等腰三角形的边长构成一个直角三角形，可以应用勾股定理：h² + (b/2)² = a²。从这个方程中解出h，即h = √(a² - (b/2)²)。然后将底b和高h代入面积公式，得到面积 = (b × √(a² - (b/2)²)) ÷ 2。

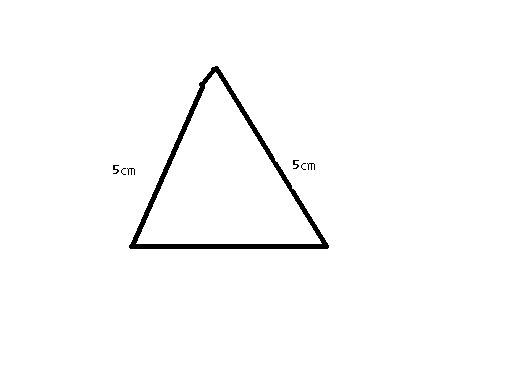
如果已知等腰三角形的顶角和底边，也可以通过三角函数来求解高。在等腰三角形中，若顶角为θ，则底边的一半与高的夹角为θ/2。根据正弦函数的定义，sin(θ/2) = h / a。由此，可以解出高h = a × sin(θ/2)。再将底b和高h代入面积公式，得到面积 = (b × a × sin(θ/2)) ÷ 2。

除了上述方法，还有一些特殊情况下简化的计算方法。例如，在等腰直角三角形中，两条等边即为直角边，假设长度均为a，底边（斜边）长度可通过勾股定理求得为√(2)a，但此时我们并不需要知道斜边的确切长度来计算面积，因为面积可以通过直角边直接计算：面积 = (a × a) ÷ 2 = a² / 2。在等腰直角三角形中，面积计算更为简单直接。

此外，如果等腰三角形是以底边和顶角的形式给出的，还可以通过海伦公式来计算面积，尽管这种方法相比前面的方法更为复杂。海伦公式适用于所有类型的三角形，其公式为：面积 = √(s(s-a)(s-b)(s-c))，其中s为半周长，即s = (a + b + c) / 2。在等腰三角形中，s = (2a + b) / 2。将这个值以及a和b代入海伦公式，可以计算出面积。不过，这种方法需要一定的代数运算能力，且计算过程相对繁琐，因此在实际应用中较少使用。

在等腰三角形的面积计算中，还需要注意一些特殊情况。例如，当等腰三角形的顶角为0°或180°时，它实际上退化为一条直线段，此时面积不存在。另外，当等腰三角形的底边长度为零时，它变为一个点，同样没有面积。这些特殊情况虽然在实际应用中较为罕见，但在理论上需要予以考虑。

对于等腰三角形的面积计算，还可以结合图形软件进行辅助计算。许多图形软件提供了强大的绘图和计算功能，用户可以通过绘制等腰三角形并输入其边长或角度等参数，软件将自动计算出面积。这种方法直观且准确，特别适合需要频繁进行几何计算的场合。

在实际应用中，等腰三角形的面积计算具有广泛的应用价值。例如，在建筑设计中，等腰三角形常用于屋顶、墙面等结构的形状设计。通过计算等腰三角形的面积，可以确定所需材料的数量，从而有效控制成本。在物理学中，等腰三角形也常用于描述某些物理现象或模型的形状特征。通过计算其面积，可以更深入地理解这些现象或模型的性质和行为。

此外，等腰三角形的面积计算还可以用于解决一些数学问题。例如，在求解某些几何问题的过程中，可能需要计算等腰三角形的面积来得到最终答案。此时，掌握等腰三角形面积的计算方法就显得尤为重要。

总之，等腰三角形的面积计算是几何学中的一项基本技能。通过掌握不同的计算方法，读者可以更全面地理解和应用等腰三角形的面积计算。在实际应用中，可以根据具体情况选择最适合的方法进行计算，以确保结果的准确性和可靠性。同时，也可以结合图形软件进行辅助计算，以提高计算效率和准确性。希望本文的介绍能够帮助读者更好地掌握等腰三角形面积的计算方法，为今后的学习和工作打下坚实的基础。