如何计算直角三角形的面积?使用什么公式?
在几何学的广阔天地里,直角三角形以其独特的性质和广泛的应用,成为连接基础与进阶知识的桥梁。其中,直角三角形的面积计算公式,虽看似简单,却蕴含着丰富的数学思想和实际应用价值。今天,我们就从多个维度出发,深入探索这一公式的奥秘。

一、公式概览:简洁之美
直角三角形的面积计算公式,直观且简洁:面积 = (底 × 高) ÷ 2。这个公式几乎在每个学生的数学课本中都能找到,它像是一把钥匙,打开了理解三角形面积计算的大门。公式的简洁性不仅便于记忆,更体现了数学语言的精炼与高效,是数学之美的一种体现。
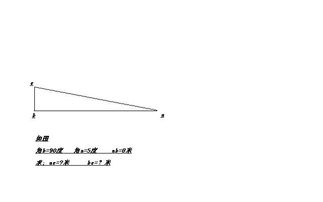
二、几何视角:直观理解
从几何学的角度来看,直角三角形的面积计算有着直观的图形解释。想象一个直角三角形,其中一条直角边作为底,另一条直角边则为高。当我们沿着这两条边分别做平行线,直至它们相交形成一个小矩形时,不难发现,这个小矩形的面积恰好是直角三角形面积的两倍。这是因为,小矩形由两个与原直角三角形全等的三角形组成。通过这一直观的几何构造,我们可以深刻理解面积公式中“底乘以高”的乘积为何需要除以2。

三、代数推导:逻辑的力量
除了直观的几何理解外,直角三角形的面积公式还可以通过代数方法进行推导。以勾股定理为基础,我们可以设定直角三角形的两条直角边分别为a和b,斜边为c。虽然直接利用勾股定理无法直接求出面积,但结合面积与边长关系的探索,可以发现,当我们将直角三角形的两条直角边视为矩形的相邻两边时,所围成的矩形面积(虽然实际上并不完全重合,但便于思维构建)为a×b。然而,这个矩形面积中包含了两个直角三角形的面积,因此,单个直角三角形的面积就是(a×b)÷2。这一过程展示了数学逻辑推理的力量,也是代数与几何相互融合的美妙体现。

四、实际应用:生活的智慧
直角三角形的面积计算公式不仅仅停留在理论层面,它在日常生活中有着广泛的应用。从建筑设计中的屋顶斜面积计算,到土木工程中的地基稳定性分析,再到简单的园艺规划中的围栏设计,几乎处处都能见到它的身影。例如,在修建一个带有斜屋顶的小屋时,工程师需要准确计算屋顶的面积,以便购买足够的防水材料。这时,直角三角形的面积计算公式就成了不可或缺的工具。此外,在农业灌溉系统的布局中,也需要利用这一公式来确保每一块田地都能得到均匀的水量覆盖。
五、教育意义:思维的启蒙
对于学生而言,学习直角三角形的面积计算公式不仅仅是掌握了一个知识点,更是数学思维能力的一次重要启蒙。通过这个公式的学习,学生可以学会如何将抽象的概念转化为直观的图形,以及如何利用已知条件进行逻辑推导。更重要的是,这一过程培养了学生的空间想象力、问题解决能力和创新思维。它让学生明白,数学不仅仅是数字和符号的游戏,更是解决现实问题、探索未知世界的强大工具。
六、文化视野:跨越时空的传承
直角三角形的面积计算公式,作为数学史上的一颗璀璨明珠,承载着人类文明的智慧与传承。从古埃及人利用三角形的性质进行土地测量,到古希腊数学家毕达哥拉斯提出勾股定理,再到中世纪欧洲数学家对三角形面积计算方法的不断完善,这一公式的形成与发展,是人类对数学世界不断探索与追求的结果。它跨越了地域、文化和时代的界限,成为了全人类共同的宝贵财富。
结语
综上所述,直角三角形的面积计算公式以其简洁性、直观性、逻辑性、实用性和教育意义,在数学领域中占据着举足轻重的地位。它不仅是连接几何与代数的桥梁,更是人类智慧与创新精神的体现。通过深入学习这一公式,我们不仅能够掌握一种计算方法,更能领略到数学之美、感受到数学的魅力所在。在未来的学习与生活中,让我们继续怀揣对数学的热爱与探索精神,勇攀数学高峰,创造更加辉煌的成就。
-
 三角形面积公式是什么(小学五年级必知)资讯攻略11-03
三角形面积公式是什么(小学五年级必知)资讯攻略11-03 -
 直角三角形的面积该怎么计算?求公式!资讯攻略10-27
直角三角形的面积该怎么计算?求公式!资讯攻略10-27 -
 三角形面积的计算方法资讯攻略11-03
三角形面积的计算方法资讯攻略11-03 -
 等腰三角形面积如何计算?资讯攻略11-30
等腰三角形面积如何计算?资讯攻略11-30 -
 轻松学会:等边三角形面积计算方法资讯攻略11-15
轻松学会:等边三角形面积计算方法资讯攻略11-15 -
 半圆面积的计算公式是什么?资讯攻略10-29
半圆面积的计算公式是什么?资讯攻略10-29











