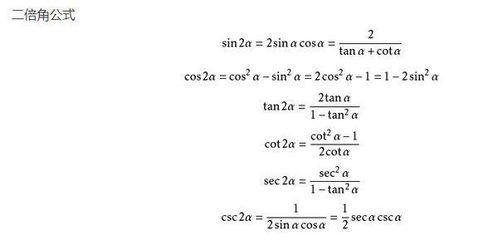三角函数常见公式概览
在数学的浩瀚宇宙中,三角函数作为一座璀璨的星座,不仅点亮了几何与代数的交汇点,更是科学、工程、物理等多个领域不可或缺的基石。想要在这片星辰大海中航行得更加自如,掌握三角函数常见公式无疑是每位探索者的必修课。今天,就让我们一同揭开三角函数的神秘面纱,细数那些能让你在数学旅途中如虎添翼的神奇公式。
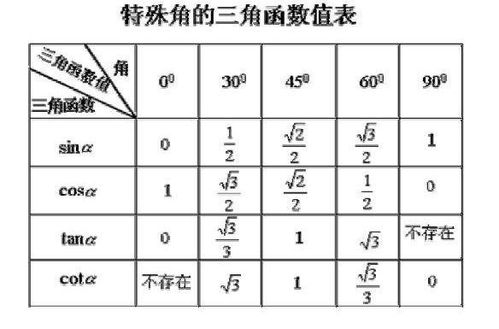
初识三角函数:定义与基础
三角函数,顾名思义,是基于三角形的函数关系,主要包括正弦(sin)、余弦(cos)、正切(tan)、余切(cot)、正割(sec)和余割(csc)六大类。它们的核心在于任意角的定义,不再局限于直角三角形的边长比,而是扩展到了单位圆上的坐标值。正弦值等于对边与斜边之比,余弦值等于邻边与斜边之比,正切值则是正弦除以余弦,这些基本定义是三角函数世界的起点。
角度与弧度的桥梁
在学习三角函数公式前,理解角度与弧度之间的转换至关重要。弧度制以半径为基准,一个完整圆周的弧度数为2π,而直角则对应于π/2弧度。这一转换不仅简化了三角函数的微积分运算,更揭示了圆周运动与三角函数之间的内在联系。掌握“角度×π/180=弧度”这一转换公式,是通往更高层次数学理解的钥匙。
三角函数的基本恒等式
三角函数的世界里,有几组基本恒等式如同灯塔般指引着方向,它们分别是:
1. 同角三角函数的基本关系:sin²θ + cos²θ = 1,tan²θ + 1 = sec²θ,1 + cot²θ = csc²θ。这些公式揭示了三角函数之间的内在联系,是化简和证明的基础。
2. 诱导公式:利用周期性、奇偶性及对称性,可以将任意角度的三角函数值转化为已知角度的值。例如,sin(π - α) = sinα,cos(π - α) = -cosα,这些公式在处理复杂角度时尤为便捷。
3. 和差化积与积化和差公式:它们是三角函数运算中的高级技巧,如sin(α + β) = sinαcosβ + cosαsinβ,cos(α + β) = cosαcosβ - sinαsinβ,通过它们,复杂的三角函数表达式可以简化为更易于处理的形式。
三角函数的倍角与半角公式
倍角公式与半角公式是三角函数运算中的两大法宝,它们将单一角度的三角函数值与复合角度的三角函数值联系起来。
倍角公式:sin2θ = 2sinθcosθ,cos2θ = cos²θ - sin²θ = 2cos²θ - 1 = 1 - 2sin²θ,tan2θ = (2tanθ) / (1 - tan²θ)。这些公式在求解周期函数问题、化简三角函数表达式时极为有用。
半角公式:sin(θ/2) = ±√[(1 - cosθ)/2],cos(θ/2) = ±√[(1 + cosθ)/2],tan(θ/2) = ±√[(1 - cosθ) / (1 + cosθ)] = (1 - cosθ) / sinθ。半角公式在求解特定角度或处理含根号的三角函数问题时尤为有效。
三角函数的和差公式与万能公式
和差公式:不仅限于基本的sin(α ± β)和cos(α ± β),还包括tan(α ± β) = (tanα ± tanβ) / (1 ∓ tanαtanβ)等,这些公式在解决涉及多个角度的三角函数问题时,能够极大地简化计算过程。
万能公式:将sinθ、cosθ、tanθ统一表示为tan(θ/2)的函数,即sinθ = 2tan(θ/2) / [1 + tan²(θ/2)],cosθ = [1 - tan²(θ/2)] / [1 + tan²(θ/2)],tanθ = 2tan(θ/2) / [1 - tan²(θ/2)]。万能公式在处理复杂三角函数问题时,提供了一种全新的视角和解决方案。
三角函数在解决实际问题中的应用
三角函数不仅仅是纸面上的理论,它们广泛应用于实际问题中。从物理学的波动与振动,到工程学的结构分析,再到天文学的星体位置计算,三角函数无处不在。例如,利用正弦定理和余弦定理解决三角形边长与角度问题,在测量、航海、建筑等领域发挥着不可替代的作用。此外,在信号处理、图像处理等现代科技领域,傅里叶变换等基于三角函数的数学工具更是发挥着核心作用。
结语:掌握公式,探索无限可能
三角函数的世界既深邃又广阔,每一组公式都是前人智慧的结晶,它们不仅是解题的工具,更是探索未知世界的钥匙。从基础的恒等式到复杂的倍角、和差公式,再到实际应用中的灵活应用,每一步都充满了挑战与乐趣。在这个旅程中,你将学会如何将抽象的概念转化为解决具体问题的力量,体验到数学之美。
现在,你是否已经迫不及待想要深入探索这个充满奥秘的领域了呢?记住,每一个公式都是一座桥梁,连接着已知与未知,引领着你走向更加宽广的数学天地。拿起你的笔,跟随三角函数的指引,开启一场充满智慧与发现的旅程吧!
- 上一篇: 5月27日蚂蚁庄园小课堂:今日答案揭晓,你答对了吗?
- 下一篇: 轻松学会!家常海鲜汤的完美制作方法
-
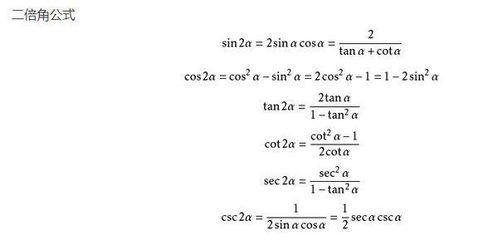 精通常见三角函数积分:公式推导与全面总结资讯攻略11-18
精通常见三角函数积分:公式推导与全面总结资讯攻略11-18 -
 如何计算直角三角形的面积?使用什么公式?资讯攻略10-24
如何计算直角三角形的面积?使用什么公式?资讯攻略10-24 -
 Excel轻松计算年龄的函数公式资讯攻略11-17
Excel轻松计算年龄的函数公式资讯攻略11-17 -
 Excel中如何进行数值相减的函数公式是什么?资讯攻略12-05
Excel中如何进行数值相减的函数公式是什么?资讯攻略12-05 -
 Excel轻松计算年龄公式资讯攻略11-17
Excel轻松计算年龄公式资讯攻略11-17 -
 如何在Excel中根据出生年月计算年龄公式?资讯攻略11-16
如何在Excel中根据出生年月计算年龄公式?资讯攻略11-16