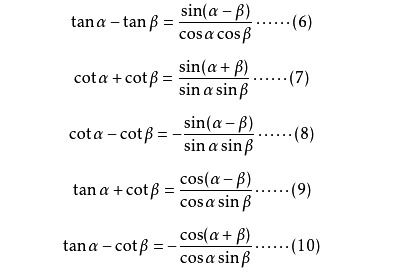高中数学必备：全面三角函数公式集锦（终极版）

在数学学习的浩瀚星空中，三角函数如同一颗璀璨的星辰，不仅照亮了几何与代数的交汇之路，更是高中数学考试中的重点与难点。为了帮助广大考生更好地掌握这一领域，本文精心整理了一份“高中数学三角函数公式大全”，力求以最通俗易懂的方式，带你领略三角函数的魅力，让备考之路更加顺畅。

一、三角函数的基本概念

首先，让我们从基础出发，理解三角函数的基本定义。三角函数主要基于直角三角形，通过边长与角度的关系来描述形状与大小。在直角三角形ABC中，设∠C=90°，A、B为锐角，则有：

正弦（sine）：sinA = 对边/斜边 = BC/AB

余弦（cosine）：cosA = 邻边/斜边 = AC/AB

正切（tangent）：tanA = 对边/邻边 = BC/AC

此外，还有余切（cotangent）、正割（secant）、余割（cosecant）等，它们分别是正切的倒数、余弦的倒数、正弦的倒数，但在高中数学中，前三个是最常用的。

二、基本关系式与恒等式

基本关系式

1. 同角三角函数的基本关系：

sin²A + cos²A = 1

1 + tan²A = sec²A

1 + cot²A = csc²A

这些关系式揭示了同一角度下不同三角函数之间的内在联系，是解题的关键。

诱导公式

三角函数具有周期性，通过诱导公式，我们可以将任意角的三角函数值转化为已知角度的函数值。例如：

sin(π - A) = sinA

cos(π - A) = -cosA

tan(π - A) = -tanA

以及利用对称性、互补性等性质推导出的其他诱导公式，它们大大简化了复杂角度的计算。

和差化积与积化和差公式

这些公式在处理两个角的三角函数运算时非常有用，比如：

sin(A + B) = sinAcosB + cosAsinB

cos(A + B) = cosAcosB - sinAsinB

以及它们的逆运算，即积化和差公式，它们为三角函数的变形和求解提供了强大的工具。

三、倍角公式与半角公式

倍角公式

通过倍角公式，我们可以将一个角的三角函数值表示为该角两倍角的函数值，如：

sin2A = 2sinAcosA

cos2A = cos²A - sin²A = 2cos²A - 1 = 1 - 2sin²A

tan2A = (2tanA)/(1 - tan²A)

这些公式在求解特定角度或简化表达式时非常有用。

半角公式

与倍角公式相反，半角公式允许我们通过原角的三角函数值来求解其一半角的值：

sin(A/2) = ±√[(1 - cosA)/2]

cos(A/2) = ±√[(1 + cosA)/2]

tan(A/2) = (1 - cosA)/sinA = sinA/(1 + cosA)

注意，这里的正负号取决于A/2所在的象限。

四、万能公式与辅助角公式

万能公式

万能公式，又称Weierstrass公式，通过引入一个辅助角t，使得所有三角函数都能表示为t的有理函数。虽然在实际解题中不常直接使用，但它展示了三角函数的深刻统一性。

辅助角公式

辅助角公式常用于将形如asinA + bcosA的表达式转化为单一三角函数的形式，便于求解最大值、最小值或化简表达式。具体形式为：

asinA + bcosA = √(a² + b²)sin(A + φ)，其中tanφ = b/a

通过调整φ的值，我们可以使表达式达到最简形式。

五、反三角函数的性质与计算

反三角函数是三角函数的逆运算，包括反正弦（arcsin）、反余弦（arccos）、反正切（arctan）等。它们满足：

如果sinθ = x，则arcsinx = θ，且-π/2 ≤ θ ≤ π/2

如果cosθ = x，则arccosx = θ，且0 ≤ θ ≤ π

如果tanθ = x，则arctanx = θ，且-π/2 < θ < π/2

反三角函数的计算通常需要使用计算器，但在某些特定情况下，可以通过三角函数的性质进行估算或求解。

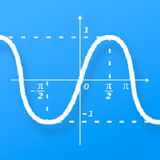
六、三角函数的图像与性质

三角函数的图像是研究其性质的重要工具。正弦和余弦函数具有周期性，周期为2π，图像分别呈波浪形和余弦波形；正切函数则具有无穷多个间断点，周期为π，图像在每一个周期内都是上升的直线。通过图像，我们可以直观地理解三角函数的增减性、最值、对称性等性质。

七、应用实例

三角函数在解决实际问题中有着广泛的应用，如物理中的波动现象、信号处理中的傅里叶变换、工程中的三角函数曲线拟合等。在高考中，常见的题型包括求值题、证明题、应用题等，解题时往往需要结合三角函数的性质、公式进行灵活变换和求解。

结语

三角函数，这个数学世界的奇妙存在，不仅承载着几何与代数的桥梁作用，更以其独特的魅力和广泛的应用价值，成为高中数学学习中的一道亮丽风景线。通过本文的详细介绍，相信你已经对三角函数的公式体系有了更加全面而深刻的理解。在接下来的备考过程中，不妨多动手练习，将理论知识与实践相结合，让三角函数成为你攻克数学难题的得力助手。愿每位考生都能在数学的海洋里乘风破浪，直达梦想的彼岸！