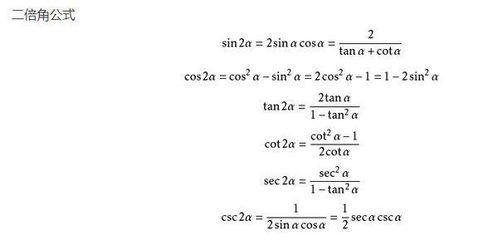三角函数cotangent的公式解析
三角函数cot,全称为余切函数,是数学中一个重要的概念,尤其在三角学和解析几何中占据举足轻重的地位。作为三角函数的一种,cot与正弦、余弦、正切等函数紧密相连,共同构成了三角函数体系。下面,我们将深入探讨三角函数cot的公式及其相关知识,以便读者能够更全面、深入地理解这一概念。
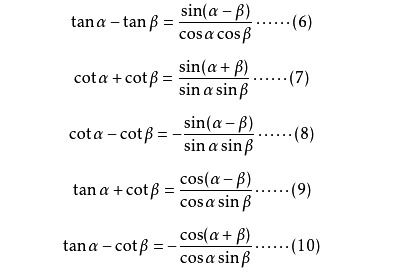
三角函数cot的定义是基于正弦和余弦函数的。具体来说,对于任意角度θ(θ≠kπ,k为整数),cotθ等于cosθ除以sinθ,即cotθ=cosθ/sinθ。这个公式揭示了cotθ与cosθ和sinθ之间的内在联系,也是求解cotθ值的基本方法。
在直角三角形中,cotθ有着直观的几何意义。设直角三角形ABC中,∠C=90°,∠A=θ,则AC为θ的对边,BC为θ的邻边,AB为斜边。根据三角函数的定义,sinθ=对边/斜边=AC/AB,cosθ=邻边/斜边=BC/AB。因此,cotθ=cosθ/sinθ=BC/AC,即直角三角形的邻边与对边之比。这个几何意义有助于我们直观理解cotθ的概念和性质。
接下来,我们来看cotθ的一些基本性质。首先,cotθ的值域为R(实数集),即cotθ可以是任意实数。这是因为cosθ和sinθ都可以是任意实数(在定义域内),而它们的比值也可以取任意实数。其次,cotθ具有周期性,周期为π。即对于任意整数k,cot(θ+kπ)=cotθ都成立。这个性质源于三角函数的周期性,也是cotθ的一个重要特征。此外,cotθ在θ=kπ/2(k为整数)处无定义,因为此时sinθ=0,而cosθ/sinθ的形式无法求出有效值。
为了更深入地理解cotθ,我们需要掌握一些与cotθ相关的公式和恒等式。首先,cotθ与tanθ互为倒数关系,即cotθ=1/tanθ。这个公式揭示了cotθ与tanθ之间的内在联系,也为我们求解cotθ提供了另一种方法。其次,cotθ具有诱导公式。对于任意角度θ,我们有cot(π/2-θ)=tanθ,cot(π/2+θ)=-tanθ,cot(π-θ)=-cotθ,cot(π+θ)=cotθ等。这些诱导公式帮助我们在求解cotθ时能够灵活转换角度,从而简化计算过程。
此外,cotθ还满足一些重要的恒等式。例如,cot²θ+1=csc²θ,其中cscθ为余割函数,定义为1/sinθ。这个恒等式揭示了cotθ、cscθ和1之间的数量关系,也是三角函数恒等式中的一个重要成员。另外,我们还有cot(α+β)=(cotαcotβ-1)/(cotα+cotβ)和cot(α-β)=(cotαcotβ+1)/(cotβ-cotα)等和差公式。这些公式在求解复杂角度的cot值时非常有用,可以大大简化计算过程。
在实际应用中,cotθ的公式和性质有着广泛的应用。例如,在物理学中,cotθ常用于描述光的折射和反射现象;在工程学中,cotθ被用于计算斜面的倾角和坡度;在天文学中,cotθ则用于描述天体之间的相对位置和角度关系。此外,cotθ还在三角函数积分、级数展开和微分方程等领域发挥着重要作用。
当然,在学习cotθ的过程中,我们也需要注意一些常见的误区和难点。首先,由于cotθ在θ=kπ/2(k为整数)处无定义,因此在求解cotθ时需要特别注意角度的取值范围。其次,虽然cotθ具有周期性,但在实际应用中我们往往需要根据具体情况选择合适的周期进行求解。此外,由于cotθ的公式和恒等式较多且复杂,因此在学习过程中需要多加练习和巩固以加深理解。
为了提高文章的曝光率并让读者更好地掌握cotθ的相关知识,我们可以结合一些实际例子进行说明。例如,我们可以给出一个具体的角度值(如θ=30°),然后利用cotθ的公式求出cot30°的值(即√3/3)。接着,我们可以进一步探讨cot30°在直角三角形中的应用以及它与其他三角函数之间的关系。此外,我们还可以结合一些实际问题(如计算斜面的倾角)来展示cotθ在解决实际问题中的重要作用。
综上所述,三角函数cot是数学中一个重要的概念,它具有明确的定义、直观的几何意义、丰富的性质和广泛的应用。通过学习和掌握cotθ的公式及其相关知识,我们可以更好地理解三角函数体系并解决实际问题。因此,我们应该在学习过程中注重理解和应用cotθ的概念和性质,不断提高自己的数学素养和解题能力。
- 上一篇: 如何在通信达股票软件中增加VOL - TDX均线?
- 下一篇: 掌握技巧,轻松折叠出美丽的玫瑰花
-
 揭秘:顶点公式的详细解析资讯攻略11-22
揭秘:顶点公式的详细解析资讯攻略11-22 -
 Excel中如何进行数值相减的函数公式是什么?资讯攻略12-05
Excel中如何进行数值相减的函数公式是什么?资讯攻略12-05 -
 三角形边长关系公式详解资讯攻略11-22
三角形边长关系公式详解资讯攻略11-22 -
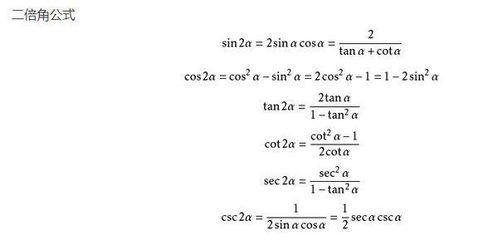 精通常见三角函数积分:公式推导与全面总结资讯攻略11-18
精通常见三角函数积分:公式推导与全面总结资讯攻略11-18 -
 余切函数的定义及公式资讯攻略11-10
余切函数的定义及公式资讯攻略11-10 -
 三角函数常见公式概览资讯攻略11-28
三角函数常见公式概览资讯攻略11-28