Q&A:轻松搞懂!如何准确区分子集与真子集?
如何区分子集和真子集

在数学的世界里,集合是一个非常重要的概念。当我们研究集合之间的关系时,经常会遇到子集和真子集这两个概念。虽然它们听起来有些相似,但实际上却有着本质的区别。本文将详细介绍如何区分子集和真子集,帮助读者更好地理解这两个概念。

一、子集的定义
首先,我们来了解一下子集的定义。

定义:如果集合A的每一个元素都是集合B的元素,那么集合A是集合B的子集。

用符号表示就是:如果对于所有的x(x属于A),都有x(x属于B),那么A⊆B。
举个例子,设A={1,2,3},B={1,2,3,4,5}。我们可以发现,集合A中的每一个元素(1,2,3)都在集合B中。因此,根据子集的定义,我们可以得出A是B的子集。
二、真子集的定义
接下来,我们来看真子集的定义。
定义:如果集合A是集合B的子集,并且集合A不等于集合B(即A中至少有一个元素不在B中),那么集合A是集合B的真子集。
用符号表示就是:如果A⊆B且A≠B,那么A⊂B。
同样地,我们用例子来说明。设A={1,2},B={1,2,3,4,5}。集合A中的元素(1,2)都在集合B中,但集合A并不包含集合B中的所有元素(比如3,4,5就不在A中)。因此,根据真子集的定义,我们可以得出A是B的真子集。
三、子集与真子集的关系
通过上面的定义,我们可以总结出子集与真子集的关系:
1. 子集:只要一个集合A的所有元素都是另一个集合B的元素,那么A就是B的子集。这里并不要求A必须小于B,也就是说A可以等于B。
2. 真子集:除了满足子集的条件外,还要求A必须小于B(即A不等于B)。也就是说,A中至少有一个元素不在B中。
四、如何判断子集和真子集
判断一个集合是否是另一个集合的子集或真子集,我们可以按照以下步骤进行:
1. 判断子集:
列出两个集合的所有元素。
检查第一个集合中的每一个元素是否都在第二个集合中。
如果第一个集合的所有元素都在第二个集合中,那么第一个集合是第二个集合的子集。
2. 判断真子集:
首先按照判断子集的方法,确认第一个集合是第二个集合的子集。
然后检查两个集合是否相等。
如果两个集合不相等,那么第一个集合是第二个集合的真子集。
五、实例分析
为了更好地理解子集和真子集的概念,我们来看几个具体的例子。
例1:设A={1,2,3},B={1,2,3,4,5}。
A的所有元素(1,2,3)都在B中,所以A是B的子集。
但A不等于B(因为B中还有4和5两个元素不在A中),所以A也是B的真子集。
例2:设A={1,2,3,4,5},B={1,2,3,4,5}。
A的所有元素(1,2,3,4,5)都在B中,所以A是B的子集。
但A等于B,所以A不是B的真子集。
例3:设A={1,2},C={1}。
A中的元素1在C中,但元素2不在C中,所以A不是C的子集。
因此,A也不可能是C的真子集。
六、子集和真子集在数学中的应用
子集和真子集的概念在数学中有着广泛的应用。以下是一些常见的应用场景:
1. 集合运算:在进行集合的并、交、差等运算时,需要判断集合之间的关系。例如,如果A是B的子集,那么A与B的并集就是B本身。
2. 逻辑推理:在逻辑推理中,我们经常需要判断命题之间的关系。例如,如果命题P是命题Q的充分条件(即如果P则Q),那么可以看作P的集合是Q的集合的子集(或真子集)。
3. 组合数学:在组合数学中,我们经常需要计算一个集合的所有子集(或真子集)的数量。这对于解决某些问题(如分配问题、排列组合问题等)非常有帮助。
4. 计算机科学:在计算机科学中
- 上一篇: 如何在百度开启历史记录功能?
- 下一篇: 如何查询宅急送快递单号信息
-
 揭秘补集:定义、表示方法及其背后的奥秘资讯攻略10-26
揭秘补集:定义、表示方法及其背后的奥秘资讯攻略10-26 -
 Q&A: 轻松掌握!如何在CAD中绘制圆锥展开图?资讯攻略11-05
Q&A: 轻松掌握!如何在CAD中绘制圆锥展开图?资讯攻略11-05 -
 Word中如何插入对号(打勾)资讯攻略11-12
Word中如何插入对号(打勾)资讯攻略11-12 -
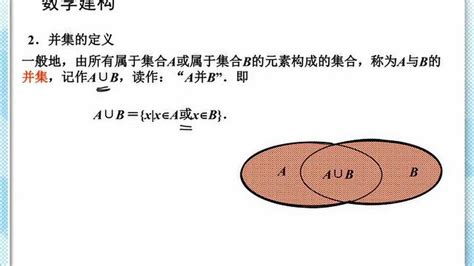 如何区分交集和并集?资讯攻略11-25
如何区分交集和并集?资讯攻略11-25 -
 明确区分:因数与倍数的差异与识别方法资讯攻略10-25
明确区分:因数与倍数的差异与识别方法资讯攻略10-25 -
 【苹果教程】Q&A:iTunes究竟是什么?如何轻松下载iTunes?资讯攻略11-11
【苹果教程】Q&A:iTunes究竟是什么?如何轻松下载iTunes?资讯攻略11-11












