如何区分交集和并集？

在探讨数学中的基本概念时，交集与并集是两个绕不开的重要话题。它们不仅在数学学科内部扮演着关键角色，还在计算机科学、逻辑学以及日常生活中的决策制定过程中发挥着重要作用。为了深入理解并准确区分这两个概念，我们需要从定义出发，逐步分析它们的性质、应用场景以及如何通过实例加深理解。

首先，我们明确交集（Intersection）的定义。在集合论的语境下，交集指的是两个或多个集合中共有的元素组成的集合。换句话说，如果你有两个集合A和B，那么它们的交集A∩B就是同时属于A和B的所有元素构成的集合。例如，假设集合A包含元素{1, 2, 3, 4}，集合B包含元素{3, 4, 5, 6}，那么它们的交集A∩B就是{3, 4}。这个定义的核心在于“共有”，即只有当某个元素同时出现在所有参与运算的集合中时，它才会出现在交集中。

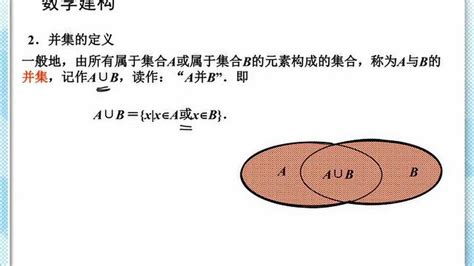
并集（Union）的概念则与交集形成鲜明对比。并集是指由两个或多个集合中所有元素（不考虑重复）组成的集合。也就是说，如果你有两个集合A和B，那么它们的并集A∪B就是属于A或属于B（或同时属于两者）的所有元素构成的集合。继续上面的例子，集合A的并集与集合B，即A∪B，将是{1, 2, 3, 4, 5, 6}。这里的关键在于“或”，即只要某个元素出现在任何一个参与运算的集合中，它就会出现在并集中。

从符号表示上来看，交集用符号“∩”表示，而并集用符号“∪”表示，这两种符号在数学文献和公式中广泛使用，是区分两者最直观的方式。

进一步分析，交集和并集具有不同的性质。交集往往导致集合元素数量的减少，因为它只包含那些在所有参与运算的集合中都出现的元素。相反，并集则可能导致集合元素数量的增加，因为它包含了所有参与运算集合中的元素，同时去除了重复项。这种性质上的差异使得交集和并集在不同的应用场景中展现出不同的价值。

在数学领域，交集和并集常用于解决集合相关问题，如求解集合的补集、判断集合的相等性、证明集合的某些性质等。在计算机科学中，交集和并集操作是数据结构和算法中的基础操作之一，广泛应用于数据库查询优化、信息检索、图论算法等领域。例如，在数据库系统中，通过计算不同数据表之间的交集和并集，可以实现数据关联查询、去重合并等功能。

逻辑学中，交集和并集的概念也有其独特的应用。在命题逻辑中，可以将命题看作集合，将命题的真值（真或假）看作集合中的元素。那么，两个命题的交集可以看作是两个命题同时为真的情况，而并集则可以看作是两个命题中至少有一个为真的情况。这种视角有助于深入理解逻辑推理中的蕴含关系、等价关系等概念。

此外，在日常生活中，交集和并集的概念也无处不在。比如，在规划活动时，我们需要确定哪些人既对活动A感兴趣又对活动B感兴趣（交集），以便制定共同的日程安排。同时，我们也需要知道哪些人对活动A或活动B感兴趣（并集），以便评估活动的总体参与度。在购物决策中，我们可能会比较不同店铺的商品清单，找出共有的商品（交集）以比较价格和质量，同时也会查看所有店铺的商品清单（并集）以寻找更多选择。

为了加深对交集和并集的理解，我们可以通过一些具体实例进行练习。例如，假设有三个集合：集合C包含所有喜欢吃苹果的人，集合D包含所有喜欢运动的人，集合E包含所有喜欢听音乐的人。那么，集合C∩D就是那些既喜欢吃苹果又喜欢运动的人组成的集合；集合C∪D则是那些喜欢吃苹果或喜欢运动（或两者都喜欢）的人组成的集合；而集合(C∩D)∪E则是那些喜欢运动且喜欢吃苹果的人，以及喜欢听音乐的人（无论他们是否喜欢运动或吃苹果）组成的集合。

通过这些实例，我们可以看到交集和并集是如何在实际问题中发挥作用的。它们不仅帮助我们精确地描述和分析问题，还为我们提供了解决问题的有效工具。

最后，值得注意的是，虽然交集和并集是集合论中最基本的概念之一，但它们并不是孤立的。在更高级的集合论和数学分支中，还涉及其他类型的集合运算，如差集、笛卡尔积、幂集等。这些运算与交集和并集一起，构成了丰富的集合理论体系，为我们提供了强大的数学工具来描述和解决各种复杂问题。

综上所述，交集和并集作为集合论中的核心概念，具有明确的定义、独特的性质和广泛的应用场景。通过深入理解这两个概念，我们可以更好地把握数学、计算机科学、逻辑学以及日常生活中的许多问题和现象。同时，通过不断练习和实践，我们可以提高自己的逻辑思维能力和问题解决能力，为未来的学习和工作打下坚实的基础。