交集与并集的符号是什么?
在数学的广阔天地里,集合论作为一门基础而重要的学科,为我们提供了理解和分析事物间关系的有力工具。其中,交集与并集作为集合运算的基本概念,不仅在日常的数学学习中频繁出现,更是解决实际问题时不可或缺的逻辑思维工具。它们各自拥有独特的符号表示,这些符号不仅仅是数学语言的一部分,更是连接抽象思维与具体操作的桥梁。本文将深入探讨交集与并集的符号是什么,以及这些符号背后的数学意义、应用场景和它们在逻辑推理中的作用。

交集符号:∩
交集,顾名思义,是指两个或多个集合中共有的元素组成的集合。在数学上,交集用符号“∩”来表示。假设我们有两个集合A和B,它们的交集记作A∩B,读作“A与B的交集”。这个符号形象地表达了从两个集合中“挑选”出共同元素的过程。

数学意义
从定义上看,A∩B包含的元素x必须同时满足x∈A且x∈B。这意味着,只有当某个元素同时属于集合A和集合B时,它才属于它们的交集。交集运算体现了集合间的一种“共同性”,是集合论中研究集合间关系的重要工具。

应用场景
交集的概念广泛应用于各个领域。例如,在数据分析中,我们可以利用交集来找出两组数据中共有的记录,这对于数据清洗、去重等预处理步骤至关重要。在生物学领域,交集可以用来识别两种或多种基因表达谱中共有的基因,从而揭示潜在的生物学通路或功能。此外,在社交网络中,交集分析可以帮助我们识别共同关注的话题或兴趣群体,促进信息的精准推送。
逻辑推理
在逻辑推理中,交集符号“∩”不仅是表达集合间关系的工具,更是构建复杂逻辑表达式的基础。通过交集运算,我们可以将多个条件合并为一个条件,从而简化问题的求解过程。例如,在解决逻辑推理题时,我们可能需要找出同时满足多个条件的对象,这时就可以利用交集运算来高效地筛选出答案。
并集符号:∪
与交集相对,并集是指两个或多个集合中所有元素(不重复计算)组成的集合。在数学上,并集用符号“∪”来表示。同样以集合A和B为例,它们的并集记作A∪B,读作“A与B的并集”。这个符号形象地表达了将两个集合中的元素“合并”在一起的过程。
数学意义
从定义上看,A∪B包含的元素x要么满足x∈A,要么满足x∈B,或者同时满足两者。这意味着,只要某个元素属于集合A或集合B(或两者都属于),它就属于它们的并集。并集运算体现了集合间的一种“包容性”,是集合论中研究集合间关系的另一种重要工具。
应用场景
并集的概念同样广泛应用于各个领域。在数据分析中,我们可以利用并集来合并多个数据集,从而得到更全面的信息。在地理信息系统(GIS)中,并集运算可以用来合并多个地理区域,生成新的地理边界。在语言学中,并集可以用来构建词汇表或语料库,通过合并多个语料资源来提高语言模型的准确性和泛化能力。
逻辑推理
在逻辑推理中,并集符号“∪”同样扮演着重要角色。通过并集运算,我们可以将多个条件合并为一个更宽泛的条件,从而扩大问题的求解范围。例如,在解决分类问题时,我们可能需要将多个类别合并为一个更大的类别,以便进行更高效的分类处理。这时,并集运算就提供了有力的数学支持。
交集与并集的相互关系
交集与并集作为集合运算的基本概念,它们之间既相互独立又相互联系。一方面,交集强调集合间的共同性,而并集则强调集合间的包容性;另一方面,交集与并集又可以相互转化。例如,对于任意两个集合A和B,它们的补集(即不属于A也不属于B的元素组成的集合)的并集等于全集(即包含所有可能元素的集合)减去它们的交集。这一性质揭示了交集与并集在更深层次上的联系。
符号背后的数学思维
交集与并集的符号不仅仅是数学语言的一部分,它们更是数学思维的具体体现。通过这些符号,我们可以将复杂的集合关系简化为简洁的数学表达式,从而更容易地进行推理和计算。这种符号化的思维方式不仅在数学领域具有广泛应用,而且也是计算机科学、物理学、经济学等多个学科中不可或缺的一部分。
结语
综上所述,交集与并集作为集合运算的基本概念,它们各自拥有独特的符号表示——交集用“∩”表示,并集用“∪”表示。这些符号不仅在数学学习中扮演着重要角色,更是解决实际问题时不可或缺的工具。通过深入理解交集与并集的概念及其符号表示,我们可以更好地把握集合间的关系,提高分析问题和解决问题的能力。同时,这些符号背后的数学思维也为我们提供了一种简洁而有效的表达方式,帮助我们更好地理解和探索世界的奥秘。
- 上一篇: 揭秘八宝粥的八大宝藏成分
- 下一篇: 李时珍是哪个朝代的人物?
-
 轻松掌握交集、并集与补集的概念资讯攻略12-01
轻松掌握交集、并集与补集的概念资讯攻略12-01 -
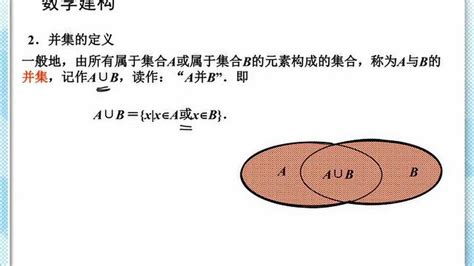 如何区分交集和并集?资讯攻略11-25
如何区分交集和并集?资讯攻略11-25 -
 打造完美圆圈图的创意指南资讯攻略11-18
打造完美圆圈图的创意指南资讯攻略11-18 -
 大耳朵图图第四季每一集的名字是什么?资讯攻略11-22
大耳朵图图第四季每一集的名字是什么?资讯攻略11-22 -
 《远方的山楂树》每一集的剧情是什么?资讯攻略11-07
《远方的山楂树》每一集的剧情是什么?资讯攻略11-07 -
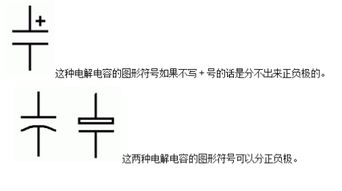 揭秘:电容的神秘符号究竟是什么?资讯攻略11-24
揭秘:电容的神秘符号究竟是什么?资讯攻略11-24












