轻松掌握交集、并集与补集的概念

在数学的广阔领域中，集合论作为基础而核心的部分，为我们提供了一种描述和分析对象集合的严谨方法。其中，交集、并集和补集作为集合论中的三大基本概念，不仅在理论研究中占据重要地位，在实际应用中也发挥着不可替代的作用。本文将围绕这三个核心概念展开，深入探讨它们的定义、性质以及在实际问题中的应用，以期为读者提供一个全面而深入的理解。

首先，我们来探讨交集的概念。交集，顾名思义，是指两个或多个集合中共有的元素所组成的集合。用数学符号表示，若A和B是两个集合，则它们的交集A∩B定义为：A∩B={x|x∈A且x∈B}。这意味着，只有当某个元素同时属于A和B时，它才属于A与B的交集。交集的性质包括：任何集合与空集的交集都是空集；若A是B的子集，则A与B的交集就是A本身；交集的运算满足交换律和结合律，即A∩B=B∩A，且(A∩B)∩C=A∩(B∩C)。这些性质使得交集在集合运算中具有重要的地位。

在实际应用中，交集的概念广泛应用于数据分析、图像处理等领域。例如，在数据分析中，我们可能需要根据某些共同特征来筛选出符合特定条件的样本数据。这时，我们可以将这些特征视为不同的集合，通过求交集的方式找到同时满足所有条件的样本数据。在图像处理中，交集的概念也被用于图像分割、特征提取等任务中。通过计算不同图像区域或特征之间的交集，我们可以实现对图像内容的更精确描述和分析。

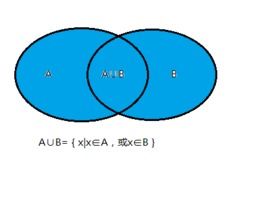
接下来，我们讨论并集的概念。与交集不同，并集是指两个或多个集合中所有元素所组成的集合。用数学符号表示，若A和B是两个集合，则它们的并集A∪B定义为：A∪B={x|x∈A或x∈B}。这意味着，只要某个元素属于A或B中的任何一个集合，它就属于A与B的并集。并集的性质包括：任何集合与空集的并集都是该集合本身；并集的运算同样满足交换律和结合律，即A∪B=B∪A，且(A∪B)∪C=A∪(B∪C)。此外，还有一个重要的性质是德摩根定律，它描述了集合的补集与交集、并集之间的关系。

并集的概念在实际应用中同样广泛。例如，在市场调研中，我们可能需要了解某个产品在不同地区的销售情况。这时，我们可以将不同地区视为不同的集合，通过求并集的方式得到该产品在所有地区的总销售情况。在数据库管理中，并集的概念也被用于数据合并、数据去重等任务中。通过计算不同数据库或数据表之间的并集，我们可以实现对数据的更全面整合和分析。

最后，我们来探讨补集的概念。补集是指在一个全集U中，不属于某个集合A的所有元素所组成的集合。用数学符号表示，若U是全集，A是U的一个子集，则A的补集A'（或称为补集U-A）定义为：A'={x|x∈U且x∉A}。补集的性质包括：任何集合的补集都是全集的子集；全集的补集是空集；补集的运算满足德摩根定律，即(A∩B)'=A'∪B'和(A∪B)'=A'∩B'。这些性质使得补集在集合运算中同样具有重要的地位。

补集的概念在实际应用中同样具有广泛的应用价值。例如，在统计学中，我们可能需要计算某个事件不发生的概率。这时，我们可以将该事件视为一个集合A，通过计算其补集A'的概率来得到该事件不发生的概率。在信息安全领域，补集的概念也被用于数据加密、数据隐藏等任务中。通过计算数据的补集或对其进行某种变换处理，我们可以实现对数据的更高级别保护。

除了单独应用外，交集、并集和补集之间还可以相互结合使用，形成更复杂的集合运算。例如，我们可以通过求一个集合的补集再与另一个集合求交集的方式，来筛选出属于某个范围但不属于另一个范围的元素。这种复合运算在实际问题中同样具有重要的应用价值。

此外，值得注意的是，虽然交集、并集和补集的概念在数学中得到了广泛的应用和深入的研究，但在实际应用中我们还需要根据具体问题的特点和需求来选择合适的集合运算方法。例如，在某些情况下我们可能需要考虑集合的势（即集合中元素的个数）或集合之间的其他关系（如包含关系、相等关系等），这时我们就需要运用更复杂的数学工具和方法来进行分析和计算。

综上所述，交集、并集和补集作为集合论中的三大基本概念，不仅在理论研究中具有重要地位，在实际应用中也发挥着不可替代的作用。通过深入理解这些概念的定义、性质以及相互之间的关系，我们可以更好地运用集合论的方法来解决实际问题。同时，随着数学和计算机科学的发展以及实际问题的不断涌现，我们也需要不断探索新的集合运算方法和应用领域，以推动数学和科学技术的进步和发展。