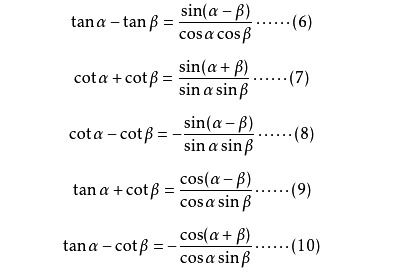用几何画板创建正弦波图形
几何画作为一种强大的工具,能够帮助我们直观地理解和构造各种几何图形和函数图像。正弦波作为一种常见的波形,在物理、工程等领域有着广泛的应用。通过几何画板,我们可以逐步构造出正弦波,从而深入理解其特性和形成原理。

首先,我们需要准备一台安装了几何画板软件的电脑。打开几何画板后,我们可以开始绘制正弦波的基础图形——圆。这是因为正弦波与圆有着密切的联系,正弦波可以看作是圆上某一点随着圆的旋转而形成的轨迹。

第一步,我们在几何画板上画一条线段r,这条线段将作为我们即将绘制的圆的半径。选中这条线段,并点击“度量/长度”工具,记录下它的长度。
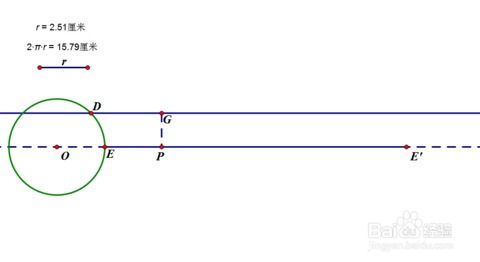
接下来,我们在画板上任意选取一个点O,这个点将作为我们圆的圆心。选中点O和之前记录的线段r的长度,点击“构造/以圆心和半径画圆”工具,这样就可以以点O为圆心,线段r为半径画出一个圆。
为了构造正弦波的轨迹,我们需要在圆上选取一个动点D。这个动点将随着我们的操作在圆上移动,形成正弦波的轨迹。同时,我们还需要选中点O和线段r,点击“构造/平行线”工具,做出线段r的两条平行线j和k。这两条平行线将作为我们构造正弦波轨迹的辅助线。
接下来,我们标记平行线k与圆Q的交点于点E。这一步是为了后续操作中找到一个固定的点,以这个点为基础进行平移和构造。
现在,我们需要计算圆的周长,这将是后续平移操作的距离。点击“度量/计算”工具,计算2*π*r的值,这个值就是圆的周长。选中计算得到的结果,点击“变换/标记距离”工具,将这个距离标记出来。
接下来,我们选中点E,点击“变换/平移”工具。在平移对话框中,选中我们之前标记的距离,固定角度改为0°,点击确定。这样,我们就可以得到点E的平移点E'。然后,我们选中点E和点E',点击“构造/线段”工具,用线段连接EE'。在EE'上,我们选取一个动点P,这个点将随着我们的操作在EE'上移动。
现在,我们选中点P和直线j,点击“构造/垂线”工具,做出过点P且垂直于直线j的垂线,交直线j于点G。然后,我们选中垂线,右键选择“隐藏垂线”,以清理画面。接着,我们选中点G和点P,点击“构造/线段”工具,用线段连接GP。最后,我们选中点G和线段GP,点击“显示/追踪对象”工具,这样,随着动点D和动点P的移动,我们将能够追踪到正弦波的轨迹。
为了更直观地展示正弦波的形成过程,我们还需要为动点D和动点P设置移动按钮。同时选中点D和点E,单击“编辑/操作类按钮/移动”选项,设置速度为“高速”,标签改为“移动点D”,建立“移动”按钮。同样地,我们为点P到点E也建立一个高速的“移动点P”按钮。
接下来,我们同时选中点P和点D,单击“编辑/操作类按钮/动画”选项。在运动属性对话框中,点P的运动方向选择“向后”,点D的运动方向选择“逆时针方向”,速度均选择“中速”,播放次数选择“只播放一次”。建立“动画按钮”,标签改为“运动点D、E”。
最后,我们依次选中“移动点D”、“移动点P”、“运动点D,P”按钮,单击“编辑/操作类按钮/系列”选项。在系列属性对话框中,执行参数选择“同时”,开始前参数选择“清除所有轨迹”。建立“系列”按钮,改标签为“正弦波”。
现在,我们只需要单击“正弦波”按钮,就可以动态地演示正弦波的形成过程了。通过观察,我们可以看到动点D在圆上逆时针旋转,同时动点P在EE'上移动,形成了正弦波的轨迹。
正弦波的形成原理可以通过几何画板上的这个构造过程得到直观的理解。正弦波是一种周期性函数,可以表示为y = A*sin(ωx + φ)的形式,其中A代表振幅,ω代表角频率,φ代表初相位,x代表时间或空间变量。在几何画板上的构造过程中,振幅A可以通过调整线段r的长度来改变,角频率ω可以通过调整动点D的旋转速度来改变,初相位φ则可以通过调整动点D的起始位置来改变。
正弦波在自然界和工程领域有着广泛的应用。例如,在振动分析中,正弦波可以用来描述物体的振动状态;在信号处理中,正弦波可以用来表示信号的频率成分;在波动分析中,正弦波可以用来描述波的传播特性。通过几何画板构造正弦波的过程
- 上一篇: 如何用手机话费积分兑换话费
- 下一篇: 淘宝退货流程全解析,轻松搞定退货!
-
 探索几何画板奇迹:轻松绘制迷人的勾股树资讯攻略01-07
探索几何画板奇迹:轻松绘制迷人的勾股树资讯攻略01-07 -
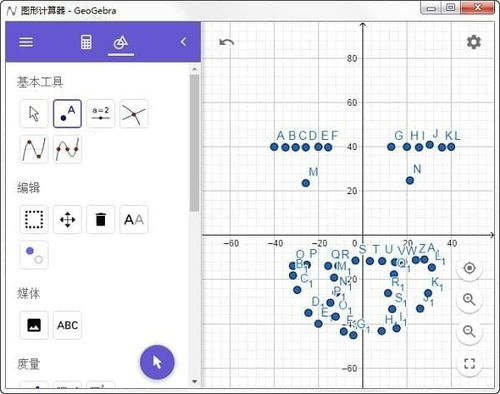 用GeoGebra图形计算器轻松绘制浪漫爱心资讯攻略11-10
用GeoGebra图形计算器轻松绘制浪漫爱心资讯攻略11-10 -
 揭秘三棱锥体积的神奇计算方法资讯攻略11-07
揭秘三棱锥体积的神奇计算方法资讯攻略11-07 -
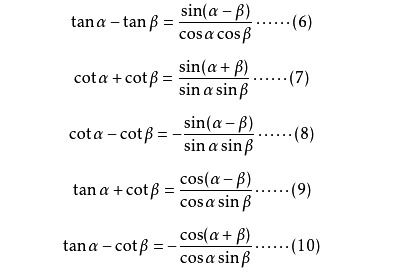 三角函数cotangent的公式解析资讯攻略11-24
三角函数cotangent的公式解析资讯攻略11-24 -
 七巧板拼长方形教程:轻松学会!资讯攻略10-28
七巧板拼长方形教程:轻松学会!资讯攻略10-28 -
 如何画出波浪线?资讯攻略11-11
如何画出波浪线?资讯攻略11-11