四棱柱的侧面展开图是什么样子的图形?
四棱柱作为一种常见的三维几何体,在日常生活和数学学习中经常出现。为了更好地理解其结构特性,我们常常需要将其侧面展开,以便直观地观察和研究。那么,四棱柱侧面展开图究竟是什么图形呢?
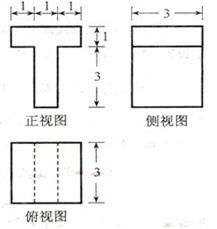
首先,我们需要明确四棱柱的基本定义。四棱柱是指一个四边形作为底面,并与另一个平行且相等的四边形顶部相连,侧面由四个矩形组成的三维几何体。这里的四边形可以是任意形状,如正方形、矩形、平行四边形等,但为了简化讨论,我们通常考虑最常见的矩形底面四棱柱,也即长方体。

当我们尝试将四棱柱的侧面展开时,可以想象沿着其高度方向,将四个侧面逐一剪开,然后平铺在一个平面上。这一过程类似于我们拆开一个纸盒子,将其侧面展开成一张纸板。在展开过程中,原本相邻的侧面会相连,形成连续的图形。

对于长方体而言,其侧面展开图非常直观。由于长方体的每一个侧面都是一个矩形,且相邻侧面之间也是矩形相连,因此其侧面展开图就是一个由四个矩形组成的平面图形。这四个矩形在展开图中依次相连,形成一个连续的矩形链或矩形网格。具体形状取决于我们如何展开,但无论哪种方式,展开图都会包含四个矩形。

如果我们将长方体的一个侧面作为起点,沿其高度方向剪开,然后依次剪开其他三个侧面,最终得到的展开图会是一个2x2的矩形网格。其中,每个小矩形都对应长方体的一个侧面。这种展开方式不仅保留了原始四棱柱的几何信息,还方便我们进行面积计算、裁剪设计等工作。
当四棱柱的底面不是矩形而是其他形状时,如平行四边形或梯形,其侧面展开图也会相应发生变化。但无论如何变化,其基本原理都是相同的:即将四棱柱的侧面逐一剪开并平铺在一个平面上。此时,展开图可能不再是一个简单的矩形网格,而是由四个形状相同或相似的平行四边形或梯形组成的连续图形。
值得注意的是,四棱柱侧面展开图的形状不仅取决于底面的形状,还取决于我们如何剪开和展开侧面。例如,对于底面为正方形的四棱柱,如果我们沿着不同的对角线方向剪开侧面,得到的展开图将是不同的。一种可能的展开图是一个大的矩形,其中包含四个小的正方形作为侧面;另一种可能的展开图则是一个由四个三角形和一个正方形组成的复杂图形。
此外,四棱柱侧面展开图在几何学和实际应用中都具有重要意义。在几何学中,通过研究侧面展开图,我们可以更直观地理解四棱柱的表面积、周长等几何量。例如,通过将侧面展开图进行裁剪和拼接,我们可以计算出四棱柱的表面积;通过测量展开图中各部分的长度和角度,我们可以推导出四棱柱的各种几何性质。
在实际应用中,四棱柱侧面展开图同样发挥着重要作用。例如,在包装设计中,我们常常需要根据产品的形状和大小来设计合适的包装盒。此时,通过绘制四棱柱侧面展开图,我们可以准确地确定包装盒的尺寸和形状,从而确保产品能够完美地放入其中。此外,在建筑设计、机械制造等领域中,四棱柱侧面展开图也被广泛应用于图纸绘制、材料裁剪等方面。
然而,需要注意的是,虽然四棱柱侧面展开图为我们提供了一种直观理解四棱柱结构的方法,但它并不是唯一的表示方式。在实际应用中,我们还需要结合其他几何表示方法(如立体图、透视图等)来全面理解四棱柱的性质和特点。
综上所述,四棱柱侧面展开图是一个由四个矩形(或其他四边形)组成的平面图形,其形状取决于底面的形状和展开方式。通过研究侧面展开图,我们可以更深入地理解四棱柱的几何特性和实际应用价值。同时,我们也需要认识到侧面展开图只是表示四棱柱的一种方法之一,应用中在实际还需要结合其他表示方法进行综合分析和应用。
此外,对于四棱柱侧面展开图的研究不仅有助于我们理解其几何性质,还可以为相关领域的研究和应用提供有益的启示。例如,在包装材料的选择上,通过比较不同形状和尺寸的侧面展开图,我们可以选择最优的包装材料来降低成本和提高效率;在建筑设计中,通过绘制和分析侧面展开图,我们可以优化建筑结构的布局和承重性能;在机械制造中,通过精确绘制侧面展开图并进行加工处理,我们可以制造出高精度和高质量的机械零件。
总之,四棱柱侧面展开图作为一种重要的几何表示方法,在几何学和相关应用领域中都发挥着重要作用。通过深入研究和理解其性质和应用价值,我们可以更好地应用这一工具来解决实际问题并推动相关领域的发展。
- 上一篇: 冬瓜美味烹饪秘籍,轻松做出诱人佳肴!
- 下一篇: 天津鼓楼:必游的旅游景点有哪些?
-
 圆锥的魔幻展开图绘制秘籍资讯攻略11-04
圆锥的魔幻展开图绘制秘籍资讯攻略11-04 -
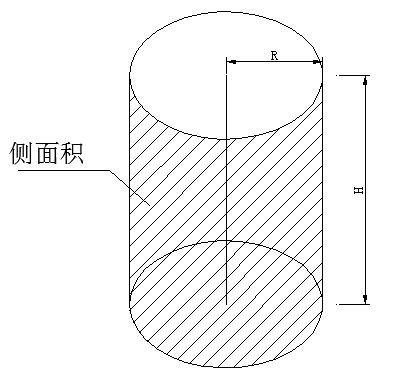 圆柱的侧面积是如何计算的?资讯攻略12-08
圆柱的侧面积是如何计算的?资讯攻略12-08 -
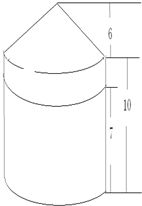 揭秘圆锥体展开图的神奇绘制法资讯攻略12-08
揭秘圆锥体展开图的神奇绘制法资讯攻略12-08 -
 长方体展开图全解析:到底有多少种变化?资讯攻略11-12
长方体展开图全解析:到底有多少种变化?资讯攻略11-12 -
 魔兽世界中的冰冻棱柱有哪些作用?详细解析其用途资讯攻略10-18
魔兽世界中的冰冻棱柱有哪些作用?详细解析其用途资讯攻略10-18 -
 腰果树是什么样子的?资讯攻略11-29
腰果树是什么样子的?资讯攻略11-29












