圆柱的侧面积是如何计算的?
圆柱的侧面积,这一数学概念,或许在初学者的眼中显得既神秘又陌生,但一旦揭开其面纱,你会发现它竟是如此直观且美妙。想象一下,你手中握着一个圆柱形的杯子,无论是喝水还是欣赏其设计,你是否曾好奇过,这个圆柱侧面展开的图形会是什么?它的面积又该如何计算?今天,就让我们一起探索圆柱侧面积的奥秘。
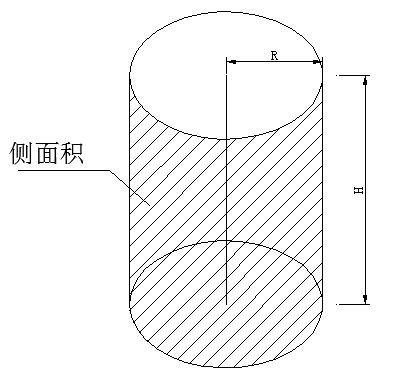
首先,我们要明确圆柱的基本构成。圆柱由一个矩形围绕其一边旋转一周而成,这条旋转的边我们称之为圆柱的高,而与之垂直的两条边则构成了圆柱的底面圆的半径。圆柱的侧面,就是由这个矩形旋转后形成的曲面。当我们尝试将这个曲面展开时,它会重新变回一个矩形,这个矩形的长就是圆柱底面的周长,而宽则是圆柱的高。

圆柱的侧面积,顾名思义,就是这个侧面的面积。由于侧面展开后是一个矩形,所以其面积计算公式就是矩形的面积计算公式:长乘以宽。在这里,“长”就是圆柱底面的周长,用公式表示为2πr(其中r为圆柱底面圆的半径),“宽”则是圆柱的高,用h表示。因此,圆柱的侧面积公式为:侧面积 = 2πrh。

这个公式简洁而有力,它揭示了圆柱侧面积与圆柱底面半径和高之间的直接关系。无论圆柱的大小、形状如何变化,只要知道了其底面半径和高,我们就可以通过这个公式迅速计算出其侧面积。
为了进一步理解这个公式,我们可以尝试通过几个实例来加深印象。比如,我们有一个底面半径为5厘米,高为10厘米的圆柱。要计算其侧面积,我们只需将底面半径和高代入侧面积公式:侧面积 = 2πrh = 2π * 5 * 10 = 100π 平方厘米。由于π约等于3.14,所以侧面积约为314平方厘米。
再比如,我们有一个底面直径为1米,高为2米的圆柱。这里需要注意的是,直径是半径的两倍,所以我们需要先将直径除以2得到半径,然后再代入公式计算。即:半径 = 直径 / 2 = 1 / 2 = 0.5米;侧面积 = 2πrh = 2π * 0.5 * 2 = 2π 平方米。同样地,将π约等于3.14代入后,侧面积约为6.28平方米。
通过这些实例,我们可以看到,圆柱的侧面积计算并不复杂,只要掌握了正确的公式和方法,就能轻松应对各种情况。
然而,圆柱的侧面积不仅仅是一个数学概念,它在现实生活中也有着广泛的应用。比如,在制作圆柱形容器时,我们需要知道其侧面积来确定所需的材料数量;在包装圆柱形物品时,我们也需要根据其侧面积来设计包装纸的尺寸;在建筑工程中,圆柱形的柱子或管道的侧面积更是计算其表面积和散热面积的重要依据。
此外,圆柱的侧面积还与一些有趣的数学问题紧密相关。比如,当我们考虑一个圆柱在空间中滚动时,其侧面的展开图形会如何变化?这个问题涉及到空间几何和动态几何的知识,对于培养我们的空间想象力和数学思维能力有着很好的帮助。
总之,圆柱的侧面积是一个既实用又有趣的数学概念。它不仅仅是一个简单的计算公式,更是连接数学与现实世界的桥梁。通过学习和掌握圆柱的侧面积知识,我们不仅可以更好地理解数学中的几何图形和面积计算问题,还可以将这些知识应用到实际生活中去,解决各种实际问题。
当然,在学习圆柱的侧面积时,我们也要注意一些常见的误区和难点。比如,有些同学可能会混淆圆柱的侧面积和底面积(或表面积),导致在计算时出现错误。为了避免这种情况的发生,我们需要明确区分这三个概念:侧面积是指圆柱侧面的面积;底面积是指圆柱底面的面积(通常有两个底面,所以总面积要乘以2);表面积则是指圆柱所有外表面的面积之和(包括两个底面和侧面)。
另外,有些同学在计算圆柱的侧面积时可能会忘记将π的值代入公式中进行计算。虽然在学习阶段我们可以使用π来表示结果以简化计算过程,但在实际应用中我们通常需要给出具体的数值结果。因此,在计算过程中我们要记得将π约等于3.14(或根据需要取更多位数)代入公式进行计算。
此外,还有一些更复杂的数学问题涉及到圆柱的侧面积计算。比如,当圆柱的侧面被切割成一个扇形或其他形状时,我们如何计算剩余部分的侧面积?这个问题需要运用到扇形的面积计算公式以及空间几何的知识来求解。虽然这类问题在初学阶段可能不会遇到太多,但对于那些对数学有浓厚兴趣并希望深入学习的同学来说,了解并掌握这些知识无疑是非常有益的。
综上所述,圆柱的侧面积是一个既基础又重要的数学概念。它不仅能够帮助我们更好地理解圆柱这一几何图形的基本性质和应用价值,还能够培养我们的数学思维和解决问题的能力。因此,在学习数学的过程中,我们应该重视圆柱的侧面积知识的学习和应用,努力掌握其基本概念、计算公式以及在实际问题中的应用方法。相信通过不断地
- 上一篇: 钱塘自古繁华,今指何地?
- 下一篇: 如何讲解英语单词'burst'的视频推荐?
-
 如何计算正方体的表面积和单个面的面积?资讯攻略11-04
如何计算正方体的表面积和单个面的面积?资讯攻略11-04 -
 如何计算9寸披萨的面积资讯攻略11-13
如何计算9寸披萨的面积资讯攻略11-13 -
 等腰三角形面积如何计算?资讯攻略11-30
等腰三角形面积如何计算?资讯攻略11-30 -
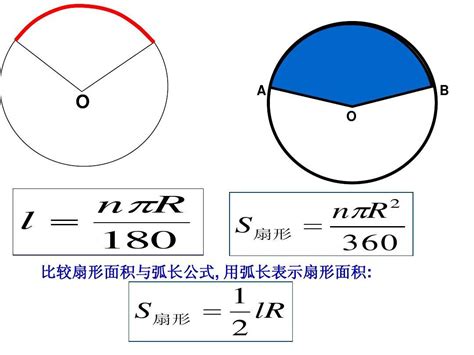 扇形面积如何计算?资讯攻略11-27
扇形面积如何计算?资讯攻略11-27 -
 如何计算直角三角形的面积?使用什么公式?资讯攻略10-24
如何计算直角三角形的面积?使用什么公式?资讯攻略10-24 -
 球的表面积计算公式及详解资讯攻略11-25
球的表面积计算公式及详解资讯攻略11-25












