扇形面积如何计算？

在数学中，扇形是一个重要的几何形状，它是圆的一部分，由两条半径以及这两条半径之间的弧所围成。计算扇形的面积，不仅可以加深对几何图形的理解，还可以在实际生活中解决诸多问题，比如计算圆锥侧面积、部分圆形区域的面积等。下面，我们将从定义、公式推导、实际应用和注意事项等多个维度来探讨扇形面积的计算方法。

定义与基本特征

扇形是圆的一部分，可以看作是一个圆被两条半径和它们之间的弧所截得的图形。这两条半径的夹角称为扇形的圆心角，通常用θ表示，单位可以是度（°）或弧度（rad）。若θ以弧度为单位，其值与圆的周长之比即为弧所对的圆心角的大小。扇形的面积与其圆心角、半径等参数密切相关。

扇形面积公式推导

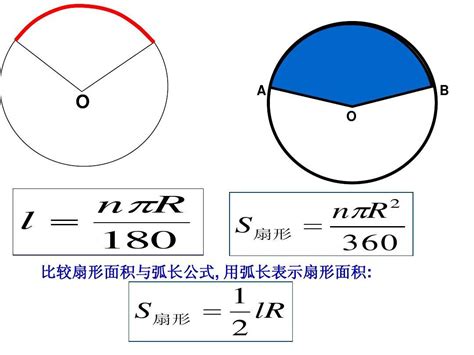
扇形面积的计算公式是基于圆的面积推导而来的。首先，圆的面积公式为A=πr²，其中r为圆的半径，π是圆周率，约等于3.14159。扇形的面积则是根据圆心角θ占整个圆（360°或2π弧度）的比例来计算的。

以角度为单位的公式推导

当圆心角θ以度为单位时，扇形面积的计算公式为：

A_扇形 = (θ/360) × πr²

这个公式的推导过程如下：

1. 圆的面积A=πr²。

2. 扇形占整个圆的比例为θ/360。

3. 因此，扇形的面积等于圆的面积乘以扇形占圆的比例，即A_扇形 = (θ/360) × πr²。

以弧度为单位的公式推导

当圆心角θ以弧度为单位时，扇形面积的计算公式为：

A_扇形 = (1/2) × θ × r²

这个公式的推导过程相对复杂，但可以通过几何图形的变换和积分的方法得到。为了简化理解，可以从物理的角度解释：将扇形看作是由无数个微小直角三角形（每个三角形的底为弧的一小段，高为半径）组成，对这些三角形的面积进行积分，即可得到扇形的面积。在弧度制下，这个积分过程简化为了(1/2) × θ × r²的形式。

实际应用

扇形面积的计算在现实生活中有着广泛的应用，以下是几个典型的例子：

圆锥侧面积的计算

圆锥是一种立体图形，它的侧面展开后是一个扇形。因此，计算圆锥的侧面积就是计算扇形的面积。圆锥的侧面积公式为：

A_侧 = πrl

其中l是圆锥的母线长，r是底面圆的半径。这里的l实际上也是扇形的半径（即圆锥斜边到圆心的距离），而扇形的圆心角θ为2π（因为圆锥侧面展开后是一个完整的圆）。将θ=2π代入扇形面积的弧度制公式，得到：

A_侧 = (1/2) × 2π × r × l = πrl

这与圆锥侧面积的公式一致。

圆形区域的面积估算

在建筑、园艺、工程等领域，经常需要估算圆形区域的部分面积。例如，设计一个圆形花坛，但只需要种植其中一部分区域的花卉。这时，可以利用扇形面积的计算方法，通过测量圆心角和半径来估算所需区域的面积。

扇形统计图

在统计学中，扇形统计图（也称为饼图）是一种常用的数据可视化工具。它通过将整个圆划分为若干个扇形区域，每个区域代表一个数据类别，扇形的面积大小反映该类别的数据占比。利用扇形面积的计算方法，可以准确地绘制扇形统计图，使数据更加直观易懂。

注意事项

在计算扇形面积时，需要注意以下几点：

1. 圆心角的单位：圆心角可以用度或弧度来表示，但计算扇形面积时，必须确保圆心角的单位与所使用的公式相匹配。如果使用角度制公式，圆心角应为度；如果使用弧度制公式，圆心角应为弧度。

2. 半径的准确性：半径是扇形面积计算中的一个重要参数，必须准确测量或给出。如果半径值不准确，将导致扇形面积的计算结果出现偏差。

3. 公式的正确应用：在计算扇形面积时，应根据具体情况选择合适的公式。例如，当圆心角以弧度为单位时，应使用弧度制公式；当需要计算圆锥侧面积时，应利用圆锥侧面展开为扇形的特性进行计算。

4. 近似值的处理：由于π是一个无理数，通常需要使用其近似值（如3.14159）进行计算。这会导致扇形面积的计算结果是一个近似值。在实际应用中，应根据精度要求选择合适的π的近似值。

5. 实际问题的复杂性：在解决实际问题时，扇形的形状和边界可能不是完全规则的。这时，可能需要通过测量、估算或数学建模等方法来近似计算扇形的面积。因此，在计算过程中应保持谨慎和灵活。

综上所述，扇形面积的计算方法涉及多个方面，包括定义、公式推导、实际应用和注意事项等。通过深入理解和掌握这些内容，可以更好地解决与扇形面积相关的数学问题和实际问题。