高效实现有向图的拓扑排序方法
在计算机科学中,有向图的拓扑排序是一个重要的概念,特别是在处理具有依赖关系的任务或活动时显得尤为重要。拓扑排序是对一个有向无环图(DAG, Directed Acyclic Graph)的所有顶点进行线性排序的过程,使得对于每一条有向边(u, v),顶点u都在顶点v之前。本文将详细介绍有向图的拓扑排序,包括其定义、应用场景、算法实现以及特殊情况的处理。
一、拓扑排序的定义
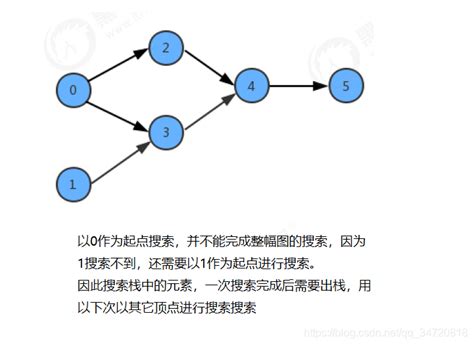
有向图是由顶点(Vertex)和边(Edge)构成的图结构,其中每条边都有方向。在有向图中,如果从一个顶点u可以沿着有向边到达另一个顶点v,则称u是v的前驱,v是u的后继。拓扑排序是指将这种有向无环图的所有顶点排成一个线性序列,使得对于每一条边(u, v),u都排在v之前。这种排序方式反映了图中顶点之间的依赖关系。
二、拓扑排序的应用场景
拓扑排序在实际应用中有广泛的用途,特别是在项目管理、任务调度和编译原理等领域。例如,在软件开发过程中,通常需要按照特定的顺序编译和链接程序的各个模块。这些模块之间的依赖关系可以用有向图来表示,其中顶点代表模块,边代表模块之间的依赖关系。通过对有向图进行拓扑排序,可以生成一个满足所有依赖关系的编译顺序。
另一个常见的应用场景是项目管理中的任务调度。假设一个项目包含多个任务,这些任务之间存在一定的先后顺序,即某些任务必须在其他任务完成之后才能开始。这种任务之间的依赖关系同样可以用有向图来表示,通过拓扑排序可以生成一个有效的任务执行顺序。
三、拓扑排序的算法实现
拓扑排序的算法有多种实现方式,其中比较常见的有基于入度的算法和基于深度优先搜索(DFS)的算法。
1. 基于入度的算法
基于入度的拓扑排序算法的基本思路是:
1. 首先,计算图中每个顶点的入度(即指向该顶点的边的数量)。
2. 然后,将入度为0的顶点加入一个栈或队列中。
3. 接下来,从栈或队列中取出一个顶点,将其加入结果序列中,并遍历该顶点的所有后继顶点,将这些后继顶点的入度减1。
4. 如果某个后继顶点的入度减为0,则将其加入栈或队列中。
5. 重复步骤3和步骤4,直到栈或队列为空。
如果最终所有顶点都被输出到结果序列中,则说明图中不存在环,否则图中存在环,无法进行拓扑排序。
2. 基于深度优先搜索的算法
基于深度优先搜索的拓扑排序算法的基本思路是:
1. 对图中的每个顶点进行深度优先搜索。
2. 在搜索过程中,对每个顶点进行访问,并将其标记为临时标记(表示该顶点正在被访问)。
3. 对于当前访问的顶点,递归地访问其所有后继顶点。
4. 当所有后继顶点都被访问后,将当前顶点标记为永久标记(表示该顶点已经被完全访问)。
5. 将永久标记的顶点按照访问的逆序加入结果序列中。
由于深度优先搜索的特性,每个顶点只会被访问一次,因此该算法的时间复杂度为O(V+E),其中V是顶点的数量,E是边的数量。
四、特殊情况的处理
在进行拓扑排序时,需要特别注意图中是否存在环。如果图中存在环,则无法进行拓扑排序,因为环中的顶点无法形成一个满足所有依赖关系的线性序列。
为了检测图中是否存在环,可以在进行拓扑排序的过程中进行判断。例如,在基于入度的算法中,如果最终还有顶点没有被输出到结果序列中,则说明图中存在环。在基于深度优先搜索的算法中,如果在搜索过程中遇到一个已经被临时标记的顶点,则说明图中存在环。
五、拓扑排序的变种和扩展
除了基本的拓扑排序外,还有一些变种和扩展的排序方式。例如,如果有向图中的边带有权重(表示任务之间的耗时或成本),则可以进行加权拓扑排序,以计算从起点到终点的最短路径或最小成本路径。此外,还可以将拓扑排序应用于并行计算中的任务调度和资源分配等问题。
六、总结
拓扑排序是一种重要的排序算法,特别适用于处理具有依赖关系的任务或活动。通过对有向无环图进行拓扑排序,可以生成一个满足所有依赖关系的线性序列。拓扑排序在项目管理、任务调度和编译原理等领域有着广泛的应用。虽然拓扑排序的算法有多种实现方式,但它们的核心思想都是基于顶点之间的依赖关系进行排序。在进行拓扑排序时,需要注意图中是否存在环,以及如何处理特殊情况。通过灵活应用拓扑排序算法,可以有效地解决各种实际问题。
通过本文的介绍,读者可以对有向图的拓扑排序有一个全面的了解,包括其定义、应用场景、算法实现以及特殊情况的处理等方面。希望这些内容能够对读者在实际应用中有所帮助。
-
 Excel表格排序技巧大揭秘:三种高效实用的方法资讯攻略10-27
Excel表格排序技巧大揭秘:三种高效实用的方法资讯攻略10-27 -
 计算机网络常见的六种拓扑结构资讯攻略10-30
计算机网络常见的六种拓扑结构资讯攻略10-30 -
 Excel中如何实现分类汇总资讯攻略11-14
Excel中如何实现分类汇总资讯攻略11-14 -
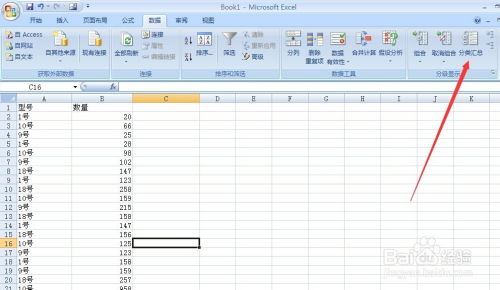 Excel中轻松实现分类汇总的方法资讯攻略11-19
Excel中轻松实现分类汇总的方法资讯攻略11-19 -
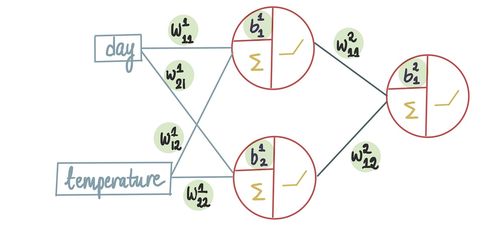 如何绘制网络图?资讯攻略12-08
如何绘制网络图?资讯攻略12-08 -
 Excel高手秘籍:轻松排序,数据内容不乱不乱!资讯攻略12-06
Excel高手秘籍:轻松排序,数据内容不乱不乱!资讯攻略12-06











