幂函数的定义域与值域详解
幂函数,作为一类基本的初等函数,在数学学习中占据着重要地位。它的一般形式为y=x^a,其中x是自变量,a是实数常数,被称为幂指数。探讨幂函数的定义域和值域,不仅能帮助我们更深入地理解这类函数的性质,还能为解决实际数学问题提供有力的工具。

定义域分析
幂函数y=x^a的定义域主要取决于幂指数a的取值。我们可以根据a的不同取值范围,将幂函数的定义域进行分类讨论。

1. 当a为正整数时:

在这种情况下,幂函数y=x^a表示x自乘a次。由于任何实数的正整数次幂都存在,因此函数的定义域为全体实数集R,即x可以取任意实数值。
2. 当a为零时:
此时幂函数变为y=x^0=1(x≠0)。根据零指数幂的定义,任何非零实数的零次幂都等于1,而0的零次幂在数学中是未定义的。因此,函数的定义域为{x|x≠0},即所有非零实数。
3. 当a为负整数时:
幂函数y=x^a此时表示x的-a次方的倒数,即y=1/x^a。由于分母x^a不能为0,因此x不能取0值。所以,函数的定义域为{x|x≠0},即所有非零实数。
4. 当a为分数时:
这种情况稍微复杂一些,需要分两步考虑。首先,当a的分子为正整数时,函数的定义域仍为非零实数集,因为任何实数的正数次幂都存在,但零的负数次幂是未定义的。其次,当a的分子为负整数时,函数形式为y=1/(x的绝对值)^|a|·(x的符号)^a,此时x可以为任意实数,因为分母永远不为零。但需要注意的是,虽然函数对所有实数都有定义,但函数值会随着x的正负而变化,具体表现为当x为正时,函数值为正;当x为负时,根据a的分母(即底数的幂次)的奇偶性,函数值可能为正也可能为负。
5. 当a为无理数时:
幂函数y=x^a在这种情况下较为复杂,但通常可以认为其定义域为全体实数集R,前提是接受实数范围内幂运算的扩展定义。不过,在一些特殊情况下(如x的π次幂),可能会涉及到复数的概念,此时函数的定义域和值域会更加复杂。
值域分析
幂函数的值域同样受幂指数a取值的影响。与定义域分析类似,我们可以根据a的不同取值范围来讨论幂函数的值域。
1. 当a为正整数时:
对于任意的x∈R,x的正整数次幂y=x^a都是非负的(当x=0时,y=0;当x>0时,y>0;当x<0且a为偶数时,y>0;当x<0且a为奇数时,y<0)。但需要注意的是,当a为偶数时,函数的值域为[0,+∞);而当a为奇数时,函数的值域为全体实数集R,因为此时负数的奇数次幂仍为负数。
2. 当a为零时:
对于非零的x∈{x|x≠0},其零次幂y=x^0=1。因此,函数的值域为{1}。
3. 当a为负整数时:
在这种情况下,幂函数y=x^a=1/x^|a|,其中x^|a|为正数(因为|a|为正整数)。因此,对于任意的非零x∈{x|x≠0},其函数值y都是正数(当x>0时)或负数(当x<0时)。所以,函数的值域为(-∞,0)∪(0,+∞),即所有非零实数。
4. 当a为分数时:
分数指数幂的值域分析需要根据底数x和指数a的具体取值来判断。例如,当a=1/2时(即开平方),对于任意的非负x∈[0,+∞),其函数值y=x^(1/2)都是非负的;而当x∈(-∞,0)时,由于负数没有实数平方根,因此函数值不存在。所以,此时函数的值域为[0,+∞)。对于其他分数指数,值域的分析可能会更加复杂,但通常可以通过分析函数的单调性和极值来确定。
5. 当a为无理数时:
无理数指数幂的值域分析通常比较困难,因为无理数本身难以精确表示和计算。但在一些特殊情况下(如e的x次幂或π的x次幂),我们可以通过研究函数的性质(如单调性、周期性等)来大致确定其值域范围。一般来说,无理数指数幂的函数值会随着x的增大而迅速增大或减小(取决于a的正负),因此其值域可能是全体实数集R或某个无界的实数区间。
综上所述,幂函数的定义域和值域受幂指数a取值的影响很大。通过分析a的不同取值范围,我们可以更准确地理解幂函数的性质和应用。同时,这种分析方法也为我们学习其他类型的函数提供了有益的借鉴和启示。
- 上一篇: 揭秘!面霜与乳液:肌肤护理中的微妙差异
- 下一篇: 揭秘:苏丹牛究竟是一种怎样的牛?
-
 掌握函数值域求解方法及经典例题解析资讯攻略11-07
掌握函数值域求解方法及经典例题解析资讯攻略11-07 -
 幂函数公式详解,水树奈奈带你轻松掌握资讯攻略11-11
幂函数公式详解,水树奈奈带你轻松掌握资讯攻略11-11 -
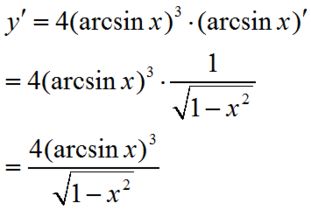 如何推导arctan函数的导数资讯攻略12-07
如何推导arctan函数的导数资讯攻略12-07 -
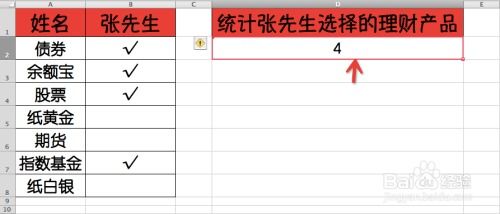 Excel 常用函数120例 —— Counta函数详解资讯攻略11-22
Excel 常用函数120例 —— Counta函数详解资讯攻略11-22 -
 对数的定义域是如何确定的?资讯攻略10-30
对数的定义域是如何确定的?资讯攻略10-30 -
 log函数的导数如何求解?资讯攻略11-10
log函数的导数如何求解?资讯攻略11-10