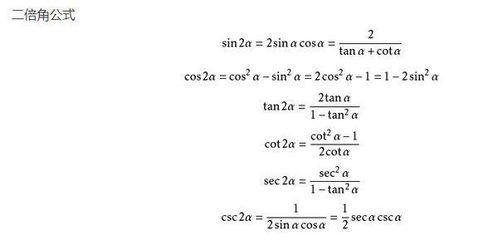如何推导arctan函数的导数

arctan的导数推导：一场数学探索之旅

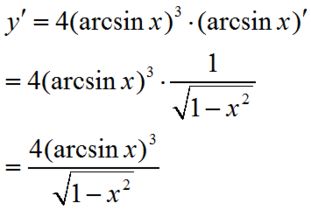
在数学的世界里，导数是一个至关重要的概念，它描述了函数值随自变量变化的速率。而对于一些特定的函数，如反正切函数arctan(x)，其导数的推导过程不仅充满了数学的美感，还蕴含着深刻的数学原理。今天，我们就来一起探索arctan函数的导数推导过程，感受数学的魅力。

一、arctan函数的定义与性质

首先，我们需要了解arctan函数的定义。arctan(x)是反正切函数，表示正切值为x的角的弧度值。其定义域为全体实数R，值域为(-π/2, π/2)。

arctan函数具有一些重要的性质，如奇函数性质：arctan(-x) = -arctan(x)，以及单调性：在定义域内，arctan(x)是单调递增的。这些性质在后续的导数推导过程中将起到关键作用。

二、导数推导的准备工作

在推导arctan函数的导数之前，我们需要掌握一些基本的微积分知识，如链式法则、反函数求导法等。

1. 链式法则：对于复合函数f(g(x))，其导数为f'(g(x)) * g'(x)。

2. 反函数求导法：如果y=f(x)的反函数为x=g(y)，则f'(x)与g'(y)互为倒数，即f'(x) = 1/g'(y)。

三、arctan函数的导数推导过程

接下来，我们正式开始推导arctan函数的导数。

方法一：直接求导法

假设y=arctan(x)，则根据反正切函数的定义，我们有x=tan(y)。

对等式x=tan(y)两边同时求导，得到：

1 = (d/dy)(tan(y)) * (dy/dx)

由于(d/dy)(tan(y)) = sec²(y)，我们可以将上式改写为：

1 = sec²(y) * (dy/dx)

接下来，我们需要将sec²(y)转化为与x有关的表达式。由于x=tan(y)，我们可以得到sec²(y) = 1 + tan²(y) = 1 + x²。

将sec²(y)替换为1 + x²，我们得到：

1 = (1 + x²) * (dy/dx)

解这个方程，我们得到arctan函数的导数公式：

(dy/dx) = 1/(1 + x²)

方法二：反函数求导法

另一种推导arctan函数导数的方法是使用反函数求导法。

我们知道，y=arctan(x)是x=tan(y)的反函数。根据反函数求导法，如果y=f(x)的反函数为x=g(y)，则f'(x) = 1/g'(y)。

在这里，f(x) = arctan(x)，g(y) = tan(y)。因此，我们需要求出tan(y)的导数g'(y)。

由于(d/dy)(tan(y)) = sec²(y)，我们可以得到g'(y) = sec²(y)。

但是，我们注意到这里的y是arctan(x)的值，因此我们需要将sec²(y)转化为与x有关的表达式。同样地，由于x=tan(y)，我们可以得到sec²(y) = 1 + tan²(y) = 1 + x²。

因此，arctan函数的导数f'(x)为：

f'(x) = 1/g'(y) = 1/(1 + x²)

四、导数公式的应用与意义

arctan函数的导数公式d/dx(arctan(x)) = 1/(1 + x²)在微积分和数学分析中有着广泛的应用。

1. 积分计算：在求解涉及arctan函数的积分时，我们可以利用这个导数公式进行换元积分或分部积分。

2. 极限求解：在求解某些涉及arctan函数的极限问题时，我们可以利用这个导数公式进行洛必达法则的应用。

3. 物理应用：在物理学中，arctan函数经常出现在描述角度、速度、加速度等物理量的公式中。其导数公式可以帮助我们求解这些物理量的变化率。

此外，arctan函数的导数公式还展示了数学中的对称性和美感。它告诉我们，无论x取何值（在定义域内），arctan(x)的斜率都是1/(1 + x²)，这个斜率随着x的增大而逐渐减小，但永远不会为零或无穷大。这种性质使得arctan函数在描述某些自然现象时具有独特的优势。

五、数学探索的乐趣与意义

推导arctan