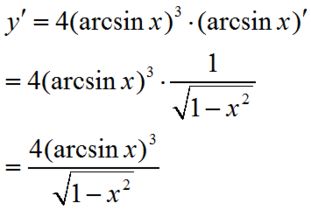对数函数的导数详解
对数函数的导数深度解析

在数学中,对数函数和导数都是极其重要的概念。对数函数描述了指数函数的反关系,而导数则是描述函数在某一点上的变化率。当我们将这两者结合时,会得到一个既深刻又实用的数学工具——对数函数的导数。

对数函数的基本形式是y=logₐx(其中a为底数,x为真数,且a>0,a≠1)。这个函数描述了以a为底x的对数值。例如,如果我们知道y=log₂8,那么y的值就是3,因为2的3次方等于8。
现在,让我们来看看对数函数的导数。在数学上,一个函数在某一点的导数表示该点处函数值的瞬时变化率。对于对数函数y=logₐx,其导数是什么呢?
首先,我们需要借助链式法则和指数函数的导数来求解。我们知道,如果y=a^x(a>0,a≠1)是指数函数,那么它的导数dy/dx=a^x*lna。现在,让我们考虑对数函数y=logₐx的反函数x=a^y。
对x=a^y两边取对数(以a为底),我们得到:
logy(a^y)=y
由于logₐa=1(任何数的以它自身为底的对数都是1),我们可以进一步化简为:
y*logy(a)=y
这表明y=1/logy(a)(当y>0时)。但是,我们注意到这里的logy(a)是一个常数,我们可以令其为C(C=1/lna,且C>0,因为a>0且a≠1)。所以,我们有:
y=Cx(其中C=1/lna)
现在,我们对y=Cx求导,得到dy/dx=C。但是,我们要求的是对数函数y=logₐx的导数,所以我们需要将y和x的关系反转回来。
由于y=logₐx和x=a^y是反函数,我们可以通过交换x和y的位置并解出y来找到对数函数的导数。从x=a^y,我们得到y=logₐx。现在,我们对x=a^y两边关于x求导(使用链式法则和指数函数的导数):
1=a^y*dy/dx*lna
解出dy/dx,我们得到:
dy/dx=1/(a^y*lna)
但是,由于y=logₐx,我们可以将a^y替换为x,得到:
dy/dx=1/(x*lna)
这就是对数函数y=logₐx的导数公式。
现在,让我们更深入地理解这个公式。首先,我们注意到这个导数公式与底数a有关。这意味着,对于不同的底数a,对数函数的导数会有所不同。但是,如果我们选择自然对数(即底数为e的对数,记作ln x),那么导数公式会变得更简单:
d/dx(ln x)=1/x
这是因为自然对数的底数e的对数值是其自身(即lne=1),所以lna=1(当a=e时),从而简化了导数公式。
此外,我们还注意到对数函数的导数是一个递减的函数。这意味着,随着x的增大,dy/dx的值会减小。这是因为对数函数在其定义域内是递增的,但增速逐渐放缓。因此,其导数(即增速)也会随着x的增大而减小。
对数函数的导数在数学和物理学中有着广泛的应用。例如,在解决与指数增长或衰减相关的问题时(如放射性衰变、人口增长等),我们经常需要使用对数函数来描述这些过程,并通过求导来找到它们的变化率。此外,在微积分、复变函数、偏微分方程等领域中,对数函数的导数也是不可或缺的工具。
除了在数学和物理学中的应用外,对数函数的导数还在工程学、经济学、生物学等领域中发挥着重要作用。例如,在工程学中,我们经常需要分析系统的稳定性或响应速度,这通常涉及到对系统函数(可能是对数函数)的求导;在经济学中,我们可能需要计算成本函数或收益函数的边际变化率(即导数),以优化资源分配或制定定价策略;在生物学中,我们可能需要研究生物种群的增长率或疾病的传播速度(这些可能涉及对数函数),并通过求导来预测未来的趋势。
最后,值得注意的是,虽然对数函数的导数公式看起来很简单(特别是对于自然对数而言),但它在数学分析中的作用却是非常深远的。它不仅为我们提供了一种计算对数函数变化率的方法,还为我们解决与对数函数相关的问题提供了一种有力的数学工具。因此,无论是对于数学专业的学生还是对于其他领域的学者来说
- 上一篇: 揭秘:“蓝瘦香菇”究竟是何含义?
- 下一篇: 晶莹剔透的美味:家常肉皮冻制作秘籍
-
 log函数的导数如何求解?资讯攻略11-10
log函数的导数如何求解?资讯攻略11-10 -
 揭秘:函数拐点的奥秘资讯攻略11-22
揭秘:函数拐点的奥秘资讯攻略11-22 -
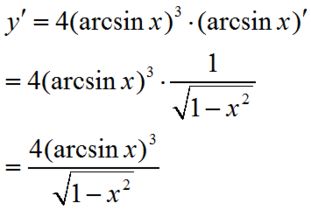 如何推导arctan函数的导数资讯攻略12-07
如何推导arctan函数的导数资讯攻略12-07 -
 掌握函数求导的实用方法资讯攻略10-29
掌握函数求导的实用方法资讯攻略10-29 -
 揭秘导数概念:一文读懂资讯攻略12-04
揭秘导数概念:一文读懂资讯攻略12-04 -
 2x的导数求解,一看就懂!资讯攻略11-06
2x的导数求解,一看就懂!资讯攻略11-06