揭秘:函数拐点的奥秘
函数的拐点:数学中的转折奥秘
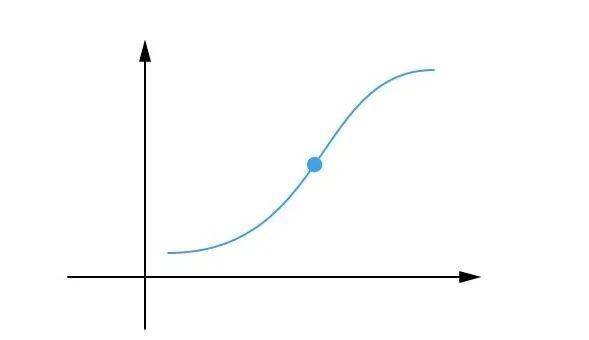
在数学的世界里,函数是描述变量之间关系的强大工具。从一次函数到复杂的指数函数、对数函数,它们以独特的形态穿梭于平面直角坐标系中,勾勒出一幅幅精妙的图案。而在这无尽的函数曲线中,有一种特殊的点,它们标志着函数图像从一种趋势向另一种趋势的转变,这便是拐点。拐点,如同函数曲线上的“转折点”,以其独特的魅力吸引着无数数学爱好者的目光。
一、拐点的定义与性质
拐点,在数学上定义为函数图像上凹凸性发生改变的点。具体来说,如果在某一点两侧,函数的二阶导数符号相反(即函数图像在这一点的一侧是凹的,而在另一侧是凸的),则该点即为拐点。为了更直观地理解这一概念,我们可以考虑一个简单的二次函数,如y=x^2。这个函数在整个定义域内都是凹的,因此它不包含拐点。然而,对于函数y=x^3,在x=0处,函数的凹凸性发生了变化:当x<0时,函数是凹的;当x>0时,函数变为凸的。因此,x=0就是该函数的一个拐点。
拐点的另一个重要性质是其局部性。这意味着拐点只影响函数在其附近的形态,而不影响整个函数的整体趋势。这一点可以从拐点的定义中看出:拐点是二阶导数变号的点,而二阶导数描述的是函数曲率的变化,这种变化通常是局部的。
二、拐点的求解方法
寻找函数的拐点,通常需要借助二阶导数。这是因为二阶导数能够揭示函数凹凸性的变化。具体来说,我们可以通过以下步骤来求解函数的拐点:
1. 求出函数的二阶导数。
2. 找出二阶导数等于0的点,以及二阶导数不存在的点(如分母为0的点)。
3. 检查这些点两侧的二阶导数符号是否相反。如果相反,则这些点就是拐点。
以函数y=x^3-3x^2+3x-1为例,我们首先求出其二阶导数:y''=6x-6。然后,我们令二阶导数等于0,解得x=1。接下来,我们检查x=1两侧的二阶导数符号:当x<1时,y''<0;当x>1时,y''>0。因此,x=1是该函数的拐点。
三、拐点的应用与意义
拐点在数学、物理、经济学等多个领域都有着广泛的应用。在数学上,拐点是函数形态分析的重要工具,它帮助我们揭示函数图像的凹凸性变化,从而更深入地理解函数的性质。在物理学中,拐点常用于描述物体的运动状态变化,如速度-时间图像中的拐点表示物体加速度的变化。在经济学中,拐点则常用于分析市场趋势的转折点,如供需曲线中的拐点预示着价格或数量的变化。
此外,拐点还具有重要的实际意义。在工程设计中,我们可能需要确保某个函数在其定义域内保持凹性或凸性,以满足特定的性能要求。这时,拐点就成为了我们设计和优化的关键。在数据分析中,拐点则常用于识别数据集中的异常值或趋势变化,从而帮助我们做出更准确的决策。
四、拐点的分类与特例
拐点根据其性质可以分为多种类型。其中,最常见的是二阶导数等于0的拐点。这种拐点在函数图像上表现为曲率的极值点,即函数图像在该点处达到最凹或最凸。除了这种常见的拐点外,还存在一些特殊的拐点。例如,对于某些分段函数或具有不可导点的函数,其拐点可能不是二阶导数等于0的点,而是二阶导数不存在的点。
此外,还有一些特殊的函数,其拐点具有独特的性质。如指数函数和对数函数,由于它们的二阶导数在整个定义域内都保持同号,因此它们不包含拐点。然而,这并不意味着这些函数没有重要的转折点。事实上,在它们的导数等于0的点处,函数的增长速度或减小速度发生了显著的变化,这些点也可以被视为函数的一种“转折点”,尽管它们不是严格意义上的拐点。
五、拐点与极值点的区别与联系
在函数的分析中,拐点与极值点是两个容易混淆的概念。为了区分它们,我们需要明确它们的定义和性质。极值点是函数值达到局部最大或最小的点,而拐点则是函数图像凹凸性发生改变的点。这意味着极值点关注的是函数值的大小变化,而拐点则关注的是函数图像的形状变化。
然而,拐点与极值点之间也存在一定的联系。在某些情况下,拐点可能伴随着极值点的出现。例如,在函数y=x^3的拐点x=0处,函数值达到局部最小(虽然这个最小值不是全局最小)。此外,在求解拐点的过程中,我们也需要用到求导数的方法,这与求解极值点的方法类似。
六、结语
拐点,作为函数图像上的特殊点,以其独特的性质和应用价值吸引着我们的关注。通过深入研究拐点的定义、性质、求解方法以及应用,我们不仅能够更好地理解函数的形态和性质,还能够将这些知识应用于实际问题的解决中。无论是数学研究、物理分析还是经济学预测,拐点都扮演着重要的角色。因此,掌握拐点的相关知识对于我们提高数学素养、解决实际问题具有重要意义。希望本文能够帮助读者更好地理解和应用拐点这一概念,从而在数学的海洋中探索出更多的奥秘。
- 上一篇: 揭秘:oioioi梗的由来与流行秘密
- 下一篇: 掌握编程:从零开始的自学秘籍
-
 什么是高等数学入门中的曲线拐点?如何求解?资讯攻略11-20
什么是高等数学入门中的曲线拐点?如何求解?资讯攻略11-20 -
 揭秘:拐点究竟是一个位置点还是坐标标识?资讯攻略12-03
揭秘:拐点究竟是一个位置点还是坐标标识?资讯攻略12-03 -
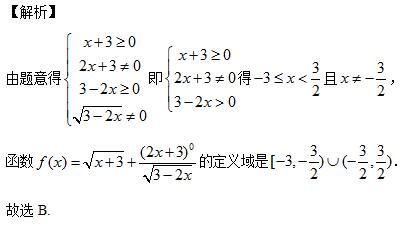 log函数的定义域是什么资讯攻略11-29
log函数的定义域是什么资讯攻略11-29 -
 探寻三角函数解析式的求解策略资讯攻略11-25
探寻三角函数解析式的求解策略资讯攻略11-25 -
 打勾函数的定义与概述资讯攻略11-29
打勾函数的定义与概述资讯攻略11-29 -
 幂函数公式详解,水树奈奈带你轻松掌握资讯攻略11-11
幂函数公式详解,水树奈奈带你轻松掌握资讯攻略11-11