log函数的定义域是什么

在数学的浩瀚宇宙中，有一个函数以其独特的魅力和广泛的应用，成为了无数学者和工程师探索的焦点。它，就是log函数，一个看似简单却蕴含着无限奥秘的数学工具。那么，你是否曾经好奇过，log函数的定义域究竟是什么？这个看似简单的问题，实则隐藏着数学逻辑的严谨与美妙。今天，就让我们一同揭开log函数定义域的神秘面纱，探索它背后的数学奥秘。

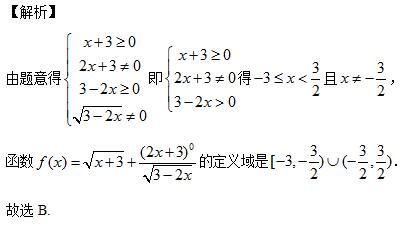
首先，我们需要明确一点，log函数，即对数函数，是数学中的一个重要概念。它表示以某个数为底，另一个数的对数。简而言之，如果a^x=N（a>0，且a≠1），那么数x叫做以a为底N的对数，记作x=logₐN。这里，a叫做对数的底数，N叫做真数。然而，并不是所有的N都能满足这个等式，也就是说，log函数的定义域并不是任意的。

为了深入理解log函数的定义域，我们首先要了解对数的发明背景。对数的概念最早由苏格兰数学家约翰·纳皮尔在1614年提出，他在著作《奇妙的对数表的描述》中，介绍了对数和对数表的使用方法。对数的发明，可以说是一场数学革命，它极大地简化了乘除运算，将复杂的运算转化为简单的加减运算，从而推动了科学计算的飞速发展。然而，这场革命的背后，是对数函数定义域的严格限制。

那么，log函数的定义域究竟是什么呢？答案很简单，却又充满了深意。对于任意的对数函数logₐN（a>0，且a≠1），其定义域是N>0，即真数N必须大于0。这个限制看似苛刻，实则合理。因为如果N小于或等于0，那么将不存在一个实数x，使得a^x=N成立。换句话说，只有当N大于0时，我们才能找到一个唯一的实数x，作为以a为底N的对数。

这个定义域的设定，不仅保证了对数函数的唯一性，还使得对数函数在实数范围内具有良好的性质。例如，对于任意的正数N1和N2，以及任意的正实数a（a>0，且a≠1），我们有：

logₐ（N1*N2）=logₐN1+logₐN2（乘法性质）

logₐ（N1/N2）=logₐN1-logₐN2（除法性质）

logₐ（N^b）=b*logₐN（指数性质）

这些性质使得对数函数在数学分析、代数、几何等多个领域都有着广泛的应用。例如，在复变函数中，对数函数是解析函数的基本例子之一；在概率论中，对数函数常用于描述随机变量的分布；在金融领域，对数函数则用于计算复利和贴现率等。

此外，对数函数还与数学中的其他重要概念紧密相连。例如，指数函数与对数函数互为反函数，这意味着它们的图像关于直线y=x对称。这一性质不仅揭示了指数函数与对数函数之间的内在联系，还为求解指数方程和对数方程提供了便捷的方法。

当然，对于log函数的定义域，我们还需要注意一些特殊情况。例如，当底数a=1时，对数函数log₁N无意义，因为对于任意的x，都有1^x=1，这意味着我们无法找到一个唯一的实数x作为以1为底N的对数。同样地，当底数a小于0时，对数函数也不存在实数解，因为负数的指数运算在实数范围内没有意义。

除了这些特殊情况外，对于任意的正实数a（a>0，且a≠1）和任意的正数N（N>0），我们都可以找到一个唯一的实数x作为以a为底N的对数。这个实数x就是log函数的值域中的元素之一。需要注意的是，虽然log函数的值域是实数集R的一个子集，但不同的底数a会对应不同的值域范围。例如，当底数a=e（自然对数的底数）时，对数函数logₑN的值域就是全体实数R；而当底数a=10时，对数函数log₁₀N的值域则是所有可以表示为有限小数或无限循环小数的实数集合。

综上所述，log函数的定义域是N>0（N为真数），这一限制保证了对数函数的唯一性和良好性质。通过对数函数的定义域和值域的研究，我们可以更深入地理解对数函数在数学和科学领域中的广泛应用和重要地位。同时，这也提醒我们，在数学的学习和研究中，要时刻保持严谨的态度和敏锐的观察力，不断挖掘数学中的奥秘和美感。

最后，让我们再次回顾一下log函数的定义域：N>0。这个看似简单的条件，实则蕴含了数学逻辑的严谨与美妙。它告诉我们，在数学的世界里，每一个定义和性质都有其深刻的内涵和广泛的应用。只有当我们真正理解并掌握了这些内涵和应用时，才能在数学的学习和研究中取得更大的进步和成就。因此，让我们继续探索数学的奥秘吧！