对数函数的定义域探秘
在对数学进行深入探索的过程中,我们经常会遇到对数这一概念。对数,作为数学中的一个重要工具,不仅在理论研究中占据一席之地,还在实际应用中发挥着不可替代的作用。然而,要准确理解和运用对数,我们首先需要明确其定义域。本文旨在详细解析对数的定义域,并探讨与之相关的几个关键点,以帮助读者更好地掌握这一数学概念。

对数的定义
对数,从字面上可以理解为“数的对数”。在数学上,对数的定义基于指数。若a(a > 0,且a ≠ 1)的x次方等于N(N > 0),即a^x = N,那么x就叫做以a为底N的对数,记作x = log_a N。这个定义揭示了对数与指数之间的密切联系,即它们互为逆运算。
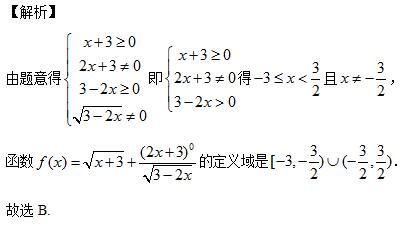
对数定义域的基本理解
在对数的定义中,有几个关键点需要注意,它们直接关系到对数的定义域:

1. 底数a的条件:底数a必须是一个大于0且不等于1的数。这是因为当a等于1时,任何数的1次方都等于1,无法唯一确定x的值;而当a小于或等于0时,由于负数或0没有实数指数幂,因此无法定义对数。
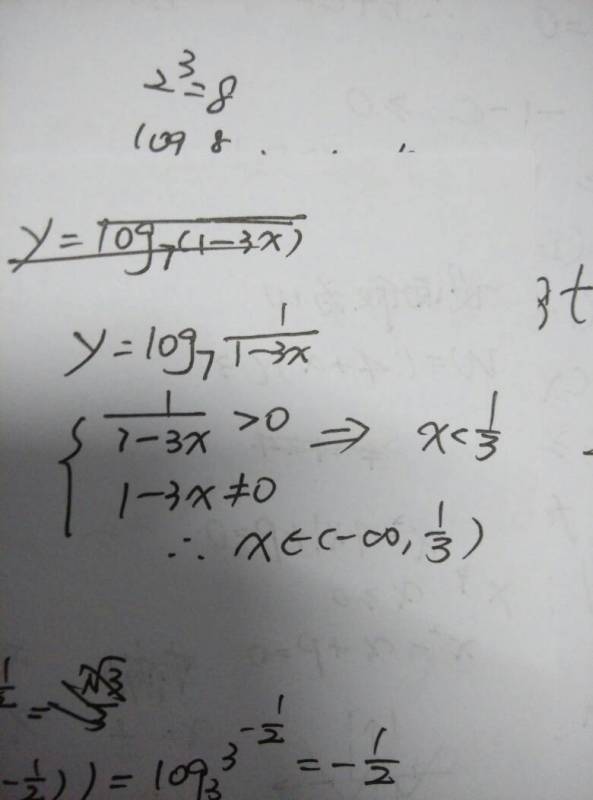
2. 真数N的条件:真数N必须是一个大于0的数。这是因为当N小于或等于0时,由于负数或0不能作为指数运算的结果(在实数范围内),因此无法找到满足a^x = N的x值。
对数定义域的详细解析
底数a的详细分析
a > 0:底数必须为正数,这是指数运算的基本要求。如果底数为负数,则无法定义其指数幂(在实数范围内)。
a ≠ 1:底数不能等于1。因为如果a = 1,那么对于任何x值,都有1^x = 1,这意味着无法唯一确定x的值来满足a^x = N(除非N也等于1,但这种情况不具有一般性)。
真数N的详细分析
N > 0:真数必须为正数。这是因为如果N小于或等于0,那么就无法找到一个实数x,使得a^x = N成立。在实数范围内,指数运算的结果总是正数(当底数为正数时),因此无法与负数或0相等。
对数定义域的应用实例
为了更直观地理解对数的定义域,我们可以通过一些实例来进行分析:
实例1:计算log_2 8。这里,底数a = 2(满足a > 0且a ≠ 1),真数N = 8(满足N > 0)。根据对数的定义,我们可以找到x = 3,使得2^3 = 8。因此,log_2 8 = 3。
实例2:判断log_(-3) 9是否有意义。这里,底数a = -3(不满足a > 0),因此无法定义log_(-3) 9。所以,这个对数表达式没有意义。
实例3:判断log_2 (-5)是否有意义。这里,底数a = 2(满足a > 0且a ≠ 1),但真数N = -5(不满足N > 0)。因此,无法找到一个实数x,使得2^x = -5成立。所以,log_2 (-5)没有意义。
对数定义域的重要性
明确对数的定义域对于正确理解和运用对数至关重要。在实际应用中,如果忽视了定义域的限制,就可能导致错误的计算结果或错误的结论。例如,在解决涉及对数的方程或不等式时,如果不考虑底数和真数的取值范围,就可能导致解集不准确或遗漏解。
对数定义域的扩展
虽然本文主要讨论的是实数范围内的对数定义域,但值得注意的是,对数的概念可以扩展到复数范围。在复数范围内,底数和真数可以是任何非零复数,但计算方法和性质会有所不同。然而,对于大多数初学者和应用场景来说,掌握实数范围内的对数定义域已经足够应对大多数问题。
结论
综上所述,对数的定义域是底数必须大于0且不等于1,真数必须大于0。这一限制条件是基于对数运算的基本性质和指数运算的要求而得出的。明确对数的定义域不仅有助于我们正确理解和运用对数,还能避免在计算和应用中出现错误。因此,在学习和运用对数时,我们应始终牢记并严格遵守这一定义域的限制。
通过对对数定义域的深入解析,我们可以更加清晰地认识到对数作为数学工具的重要性和应用广泛性。无论是在科学研究、工程技术还是日常生活中,对数都扮演着不可或缺的角色。因此,我们应该不断学习和探索对数的性质和应用,以更好地利用这一数学工具来解决实际问题。
- 上一篇: 苹果手机12如何强制关机?
- 下一篇: Excel函数计算身份证号码年龄的方法
-
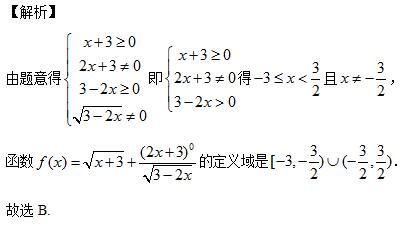 log函数的定义域是什么资讯攻略11-29
log函数的定义域是什么资讯攻略11-29 -
 对数的定义域是如何确定的?资讯攻略10-30
对数的定义域是如何确定的?资讯攻略10-30 -
 对数函数的导数详解资讯攻略10-28
对数函数的导数详解资讯攻略10-28 -
 log函数的导数如何求解?资讯攻略11-10
log函数的导数如何求解?资讯攻略11-10 -
 揭秘:函数拐点的奥秘资讯攻略11-22
揭秘:函数拐点的奥秘资讯攻略11-22 -
 探索导数:揭秘其神秘概念与精确定义资讯攻略12-06
探索导数:揭秘其神秘概念与精确定义资讯攻略12-06











