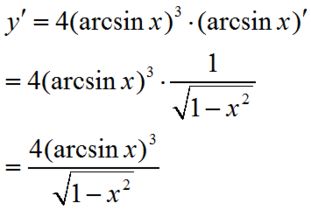探索导数:揭秘其神秘概念与精确定义
探秘导数的奇妙世界:从概念到定义的深度解析

在数学这片浩瀚无垠的宇宙中,有一个概念如同璀璨星辰般引人注目,它不仅连接了代数与几何,更是微积分学大厦的基石。这便是导数——一个看似简单却蕴含无限奥秘的数学工具。今天,就让我们一起踏上一段探索之旅,揭开导数的神秘面纱,看看它究竟是何方神圣,又是如何定义并改变我们对数学世界的认知的。

想象一下,你正驾驶着一辆汽车在高速公路上飞驰,车速仪表盘上的数字不断变化,反映着你与前方目标的接近程度。这个不断变化的速度,其实就是位移随时间变化率的一个直观体现。在数学中,这种变化率就被抽象为“导数”的概念。简单来说,导数描述的是一个函数在某一点上的瞬时变化率,它告诉我们函数值如何随着自变量的微小变化而变化。

为了更好地理解导数,让我们先从它的起源说起。早在17世纪,两位数学巨匠——英国的牛顿和德国的莱布尼茨,在解决物理学和几何学中的问题时,不约而同地发现了这个描述变化率的数学工具。牛顿用它来求解物体的瞬时速度和加速度,而莱布尼茨则更多地将其应用于曲线的切线斜率问题。尽管两人的出发点不同,但他们的工作最终汇成了微积分学这条壮阔的河流,而导数则是这条河流中最重要的成分之一。
那么,导数的定义究竟是什么呢?在严谨的数学语言中,导数被定义为函数在某一点的极限值,这个极限值描述了函数在该点附近的变化率。具体来说,如果我们有一个函数f(x),它在x0这一点可导,那么f在x0处的导数f'(x0)就是通过以下极限过程定义的:
f'(x0) = lim (h->0) [f(x0+h) - f(x0)] / h
这个定义听起来可能有些抽象,但别担心,我们可以通过一个简单的例子来加以说明。假设我们有一个线性函数f(x) = 2x + 1,它表示的是一条斜率为2的直线。根据导数的定义,我们可以计算出f在任意点x0处的导数f'(x0)都是2。这意味着,无论我们在这条直线上的哪一点观察,它的变化率(即斜率)都是恒定的,且等于2。
当然,并非所有的函数都像线性函数那样简单。在现实生活中,我们遇到更多的是复杂多变的非线性函数,如抛物线、指数函数、对数函数等。这些函数的导数往往不再是常数,而是随着x的变化而变化。但无论如何,导数总是能够捕捉到函数在某一点上的瞬时变化率,为我们提供关于函数行为的重要信息。
接下来,让我们来看看导数在实际应用中的一些精彩案例。在物理学中,导数被广泛应用于描述物体的运动状态。例如,速度是位移对时间的导数,加速度则是速度对时间的导数。通过计算这些导数,我们可以精确地了解物体在任意时刻的速度和加速度,从而预测它的运动轨迹。
在经济学中,导数也有着广泛的应用。例如,边际成本是总成本对产量的导数,它告诉我们每增加一单位产量所需增加的成本是多少。同样地,边际收益是总收益对产量的导数,它反映了每增加一单位产量所能带来的额外收益。通过比较边际成本和边际收益,企业可以制定出最优的生产计划,以实现利润最大化。
此外,导数在几何学、工程学、生物学等领域也有着广泛的应用。在几何学中,导数可以用来求解曲线的切线斜率和曲率;在工程学中,导数可以用来分析结构的应力和应变;在生物学中,导数则可以用来描述生物种群的增长率和衰减率等。
然而,导数的应用并不仅仅局限于这些具体领域。更重要的是,它为我们提供了一种全新的思维方式——用变化的观点来看待世界。通过计算导数,我们能够捕捉到事物发展的瞬间趋势和潜在规律,从而做出更加准确和科学的决策。
当然,要真正掌握导数并灵活运用它来解决实际问题,还需要我们付出大量的努力和实践。这包括深入理解导数的定义和性质、熟练掌握求导的方法和技巧、以及学会将实际问题转化为数学模型并求解等。但只要我们坚持不懈地学习和探索,就一定能够在这个奇妙的数学世界中畅游无阻。
最后,让我们回到导数的定义上来。虽然这个定义看起来有些复杂和抽象,但它却蕴含着极其深刻的数学思想和哲学意义。它告诉我们,数学不仅仅是一门关于数字和公式的学科,更是一门关于变化和规律的学科。通过数学,我们能够更好地认识和理解这个世界,从而创造出更加美好的未来。
综上所述,导数作为微积分学的核心概念之一,不仅在数学学科内部发挥着举足轻重的作用,而且在实际应用中也展现出了巨大的潜力和价值。它不仅能够描述函数在某一点上的瞬时变化率,还能够为我们提供关于事物发展趋势和潜在规律的重要信息。因此,无论你是数学爱好者、科研人员还是企业家,都应该深入学习和掌握导数这一数学工具,让它成为你探索未知世界的得力助手。
- 上一篇: 手机缴纳话费的方法
- 下一篇: 掌握模拟人生3:6大实用秘籍揭秘
-
 揭秘导数概念:一文读懂资讯攻略12-04
揭秘导数概念:一文读懂资讯攻略12-04 -
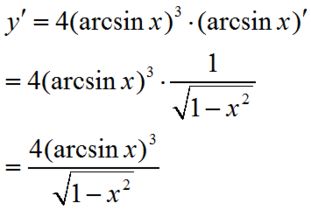 如何推导arctan函数的导数资讯攻略12-07
如何推导arctan函数的导数资讯攻略12-07 -
 探索虚数的神秘世界:定义与概念揭秘资讯攻略11-15
探索虚数的神秘世界:定义与概念揭秘资讯攻略11-15 -
 2x的导数求解,一看就懂!资讯攻略11-06
2x的导数求解,一看就懂!资讯攻略11-06 -
 慎重的精确定义及含义解析资讯攻略10-26
慎重的精确定义及含义解析资讯攻略10-26 -
 揭秘:一光年究竟有多少公里?资讯攻略11-26
揭秘:一光年究竟有多少公里?资讯攻略11-26