什么是高等数学入门中的曲线拐点?如何求解?
在高等数学中,曲线拐点是一个关键概念,它不仅在理论研究中占据重要地位,也在实际应用中发挥着重要作用。拐点,又称为反曲点,是连续曲线弧上凹与凸的分界点。简单来说,拐点是函数图像上改变曲线向上或向下方向的点,即曲线由凹变凸或由凸变凹的转折点。这一特性使得拐点成为分析函数图像形状变化的重要工具,同时也与函数的二阶导数性质紧密相关。

拐点的定义
在正式讨论拐点的求法之前,我们先来明确拐点的定义。设连续曲线y=f(x)在考察范围(a,b)内具有二阶导数,若曲线上的某一点P是凹的曲线弧与凸的曲线弧的分界点,则称点P是曲线y=f(x)的拐点。直观地说,拐点是使切线穿越曲线的点,即曲线的凹凸分界点。若该曲线图形的函数在拐点有二阶导数,则二阶导数在拐点处异号,由正变负或由负变正,或不存在。

拐点的求法
拐点的求法主要依赖于函数的二阶导数。具体步骤如下:

1. 求解函数的一阶导数和二阶导数:

首先,我们需要求出函数f(x)的一阶导数f'(x)和二阶导数f''(x)。这一步骤是求解拐点的基础,因为拐点的位置通常与二阶导数的性质密切相关。

2. 令二阶导数等于零:
接下来,我们令二阶导数f''(x)等于零,解出方程得到可能的拐点的横坐标。这一步骤是为了找到可能的拐点位置,但需要注意的是,这些解并不一定是真正的拐点,还需要进一步验证。
3. 验证拐点的存在性:
对于每个可能的拐点横坐标x0,我们需要验证f''(x)在x0左右是否异号。如果f''(x)在x0左侧为正,在x0右侧为负(或相反),则x0是该曲线的一个拐点。如果f''(x)在x0左右同号,则x0不是拐点。这一步骤是确定拐点存在性的关键。
4. 计算拐点的坐标:
一旦确定了拐点的横坐标x0,我们就可以通过代入原函数f(x)计算出对应的纵坐标y0,从而得到拐点的坐标(x0, y0)。
示例分析
为了更好地理解拐点的求法,我们可以通过一个具体的例子来进行说明。
例:求曲线y=x^2+2lnx在其拐点处的切线方程。
解:
1. 求一阶导数和二阶导数:
y'=2x+2/x
y''=2-2/x^2
2. 令二阶导数等于零:
令y''=0,解得x^2-1=0,即x=±1。但由于原函数y里面有lnx,x需要大于0,所以舍去x=-1,得到可能的拐点横坐标x=1。
3. 验证拐点的存在性:
当x<1时,y''<0;当x>1时,y''>0。因此,f''(x)在x=1左右异号,所以x=1是该曲线的一个拐点。
4. 计算拐点的坐标:
将x=1代入原函数y=x^2+2lnx,得到y=1+0=1。所以,拐点的坐标为(1,1)。
5. 求切线方程:
在拐点(1,1)处,切线的斜率等于函数在该点的导数值。将x=1代入一阶导数y'=2x+2/x,得到切线斜率为k=4。根据点斜式方程y-y1=k(x-x1),得到切线方程为y-1=4(x-1),即y=4x-3。
注意事项
在求解拐点的过程中,需要注意以下几点:
1. 符号的运用:在求解过程中需要注意符号的运用,避免求解出错。特别是在验证拐点的存在性时,要仔细判断f''(x)在拐点左右是否异号。
2. 微积分知识:求解过程需要使用到微积分知识,对于没有学过微积分的人需要提前学习。特别是二阶导数的求解和符号的判断,需要掌握一定的微积分基础。
3. 函数的复杂性:由于函数的复杂性,有些函数可能不存在拐点。这时,需要通过函数图像的观察和分析来判断。对于无法直接求解二阶导数的函数,可以尝试通过反函数或参数方程等方法进行求解。
4. 多项式函数的化简:对于多项式函数,可以通过分解因式、配方法等手段化简函数形式,使得求解拐点更加简单。
拐点的应用
拐点在数学分析、经济学、物理学等多个领域都有广泛的应用。例如,在经济学中,拐点可以用于分析经济增长的转折点;在物理学中,拐点可以用于描述物体运动的加速度变化;在工程设计中,拐点可以用于优化曲线形状以提高性能。因此,掌握拐点的定义和求法对于提高相关领域的研究水平具有重要意义。
综上所述,拐点是高等数学中一个重要的概念,它反映了函数图像的形状变化和二阶导数的性质。通过求解拐点,我们可以更深入地了解函数的性质和行为,为相关领域的研究和应用提供有力支持。
- 上一篇: 如何有效减小腹部赘肉
- 下一篇: 如何计算定期存款的利息?
-
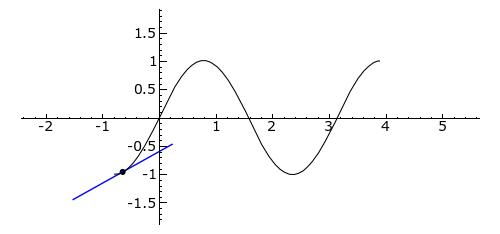 揭秘:拐点究竟是一个位置点还是坐标标识?资讯攻略12-03
揭秘:拐点究竟是一个位置点还是坐标标识?资讯攻略12-03 -
 高等数学入门:全微分方程的概念及解法资讯攻略11-11
高等数学入门:全微分方程的概念及解法资讯攻略11-11 -
 揭秘:函数拐点的奥秘资讯攻略11-22
揭秘:函数拐点的奥秘资讯攻略11-22 -
 双曲线的顶点坐标如何求解资讯攻略11-10
双曲线的顶点坐标如何求解资讯攻略11-10 -
 掌握第一类曲线积分的高效计算方法资讯攻略11-01
掌握第一类曲线积分的高效计算方法资讯攻略11-01 -
 双曲线准线绘制教程资讯攻略11-02
双曲线准线绘制教程资讯攻略11-02












