揭秘:拐点究竟是一个位置点还是坐标标识?
在数学的广阔天地里,有着各种各样的术语和概念,它们有时让初学者感到困惑。比如,“拐点”这个词,听起来既神秘又关键,让人不禁要问:拐点,到底是点还是坐标呢?为了解开这个谜团,让我们一起踏上一段探索之旅,用通俗易懂的语言,详细了解拐点的各个方面。
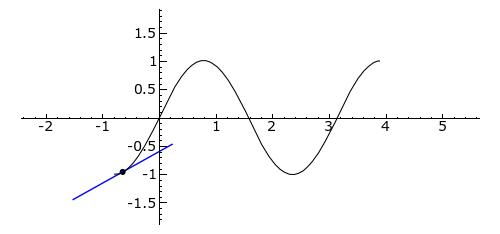
首先,我们需要明白什么是拐点。拐点,在数学上,尤其是在微积分和几何学中,是一个非常重要的概念。它描述的是曲线上一个特殊的点,这个点两侧曲线的弯曲方向是相反的。换句话说,当你沿着曲线移动,经过拐点时,你会感觉到曲线从左向右或由右向左“拐弯”了。这个“拐弯”的点,就是我们所说的拐点。

那么,拐点是点还是坐标呢?要回答这个问题,我们需要从两个方面来看:从几何图形的直观感受,以及从数学描述的精确性。

从几何图形的角度来看,拐点无疑是一个点。想象一下你手中有张曲线图,比如一个抛物线或者正弦波。你沿着曲线滑动手指,当手指滑到一个特别的位置,即曲线弯曲方向发生改变的那个点时,这个“位置”就是拐点。在这里,拐点是一个具象的点,是我们可以用眼睛看到、用手指指出的。

然而,数学是严谨的,它需要用精确的语言来描述世界。因此,在数学的描述中,拐点不仅仅是一个点,更是一个具有坐标的位置。坐标,简单来说,就是用来确定一个点在空间中的位置的数值。在二维平面上,我们用两个数值——横坐标(x)和纵坐标(y)——来确定一个点的位置。所以,当我们在数学上谈论拐点时,我们通常会说:拐点在曲线上的位置是(x₀, y₀),其中x₀和y₀分别是拐点的横坐标和纵坐标。
这样,拐点就同时具备了“点”的直观性和“坐标”的精确性。它是曲线上那个特别的点,也是具有特定坐标值的位置。
接下来,我们进一步探讨拐点的性质和如何找到它。
拐点的性质之一是它的两侧曲线的弯曲方向相反。这一点非常关键,因为它让我们能够区分拐点和其他类型的点,比如极值点(曲线局部最高或最低的点,两侧曲线弯曲方向相同)。另外,拐点还涉及到曲线的凹凸性。在拐点左侧,曲线可能是凹的(即曲线内部的点低于其两侧的点);在拐点右侧,曲线可能是凸的(即曲线内部的点高于其两侧的点)。这种凹凸性的变化,是拐点的一个重要特征。
找到拐点的方法,通常涉及到对曲线方程的分析。对于给定的曲线方程y=f(x),我们可以通过求其二阶导数f''(x)来找到拐点。二阶导数描述的是曲线斜率的变化率,也就是曲线弯曲的程度。当f''(x)=0时,我们找到了一个可能的拐点位置(注意,这里只是可能,因为还需要检查f''(x)的符号变化来确认)。然后,我们计算该位置处的坐标(x₀, f(x₀)),就得到了拐点的具体坐标。
当然,在实际应用中,拐点不仅仅是一个数学上的概念。它在很多领域都有着广泛的应用,比如经济学中的供需平衡点、物理学中的振动系统的平衡点、工程学中的结构稳定性分析等。在这些领域中,拐点往往代表着某种重要的变化或转折点,是分析和预测未来趋势的关键。
此外,拐点还与生活中的一些现象紧密相连。比如,当我们学习骑自行车时,从摇摇晃晃到平稳骑行的那个“瞬间”,就可以看作是一个拐点。在这个拐点之前,我们可能需要不断地调整平衡;而在这个拐点之后,骑自行车就变得相对容易和稳定了。同样地,在学习新技能、适应新环境或面对挑战时,我们也常常会遇到这样的拐点,它们标志着我们的成长和进步。
综上所述,拐点既是曲线上的一个点,也是具有特定坐标值的位置。它描述的是曲线上一个特殊的转折点,是数学、物理、经济等多个领域中的重要概念。通过理解和应用拐点的概念,我们可以更好地分析和预测各种现象和趋势,从而在生活和工作中做出更明智的决策。
希望这篇通俗易懂的文章能够帮助你理解“拐点是点还是坐标”的问题。拐点,就像生活中的许多事物一样,既有着直观感性的认识,也有着精确理性的描述。它既是曲线上那个特别的点,也是具有特定坐标值的数学位置。当我们掌握了拐点的概念和性质后,就能更好地利用它来探索这个充满奥秘的世界了。
- 上一篇: 美味火鸭汤的制作秘籍
- 下一篇: B站播放器功能使用技巧与经验分享
-
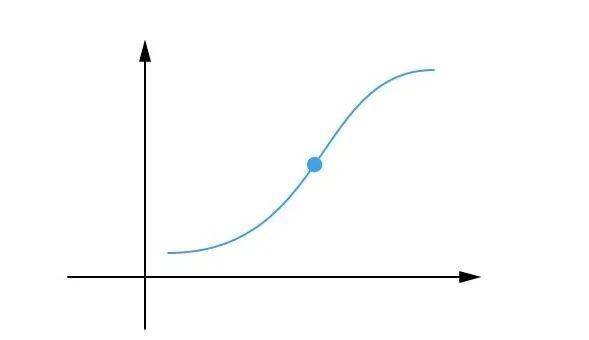 揭秘:函数拐点的奥秘资讯攻略11-22
揭秘:函数拐点的奥秘资讯攻略11-22 -
 揭秘:视频水印究竟是什么?资讯攻略11-21
揭秘:视频水印究竟是什么?资讯攻略11-21 -
 揭秘:DOI究竟是何方神圣?资讯攻略10-30
揭秘:DOI究竟是何方神圣?资讯攻略10-30 -
 如何查询并定位经纬度坐标?资讯攻略11-18
如何查询并定位经纬度坐标?资讯攻略11-18 -
 揭秘:苹果ID究竟是什么?资讯攻略10-28
揭秘:苹果ID究竟是什么?资讯攻略10-28 -
 揭秘:Z系列车型究竟是何方神圣?资讯攻略11-22
揭秘:Z系列车型究竟是何方神圣?资讯攻略11-22












