打勾函数的定义与概述

在数学的奇妙世界里，隐藏着一种独特的函数形态，它不仅在数学研究中占据了一席之地，更在经济学、物理学等多个领域展现出了非凡的应用价值。这个函数，就是人们常说的“打勾函数”——一个听起来神秘，实则充满魅力的数学存在。今天，就让我们一起揭开打勾函数的神秘面纱，探索它背后的数学奥秘与广泛应用。

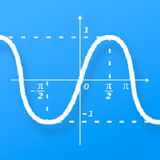
想象一下，在坐标系中，一条曲线优雅地划过，它的一端缓缓上升，另一端则缓缓下降，中间部分则形成了一个完美的“勾”形。这，就是打勾函数最直观的形象描述。在数学上，打勾函数通常指的是形如y=ax+b/x（a>0,b>0，x>0）的函数，其中a和b为常数，且x的取值范围限定在正数域。这种函数之所以被称为“打勾函数”，是因为其图像在坐标系中呈现出一种类似“√”的形状，简洁而优美。

一、打勾函数的数学特性

打勾函数的魅力，首先体现在其独特的数学特性上。它的定义域虽然限定在正数域，但在这有限的范围内，它却展现出了丰富的变化。当x的值从0开始增大时，函数值y首先会减小，到达一个最小值点后，又会开始增大。这个最小值点，就是打勾函数的一个重要特征点，它位于x=√(b/a)处，此时函数取得最小值2√(ab)。这一特性，使得打勾函数在求解某些优化问题时具有得天独厚的优势。

此外，打勾函数还具有单调性、奇偶性等数学性质。在(0,√(b/a))区间内，函数是单调递减的；而在(√(b/a),+∞)区间内，函数则是单调递增的。这一性质，使得我们能够方便地判断函数在不同区间的行为特征。同时，对于某些特定的打勾函数，如y=x+1/x，它们还具有奇函数的性质，即关于原点对称。这些数学特性，不仅丰富了打勾函数的内涵，也为我们的研究和应用提供了更多的便利。

二、打勾函数的应用价值

打勾函数的魅力，不仅仅在于其数学上的独特性，更在于它在实际应用中的广泛价值。在经济学领域，打勾函数常被用来描述某些经济现象的变化规律。例如，在成本分析中，企业可能会发现其生产成本与产量之间的关系呈现出打勾函数的特征。当产量较低时，单位成本较高；随着产量的增加，单位成本逐渐降低；但当产量达到一定程度后，由于管理费用的增加，单位成本又会开始上升。通过打勾函数，企业可以更加精确地预测和控制成本，从而制定出更加合理的生产计划。

在物理学领域，打勾函数同样有着广泛的应用。例如，在电磁学中，电荷在电场中的运动轨迹可能会受到电场力和其他力的共同作用，从而形成类似打勾函数的曲线。通过研究这种曲线，我们可以更加深入地了解电荷在电场中的运动规律，为电磁学的研究和应用提供有力的支持。

此外，在工程学、生物学等其他领域，打勾函数也有着广泛的应用。例如，在桥梁设计中，工程师需要考虑桥梁在不同荷载作用下的变形情况。通过打勾函数，工程师可以更加准确地预测桥梁的变形情况，从而确保桥梁的安全性和稳定性。在生物学研究中，打勾函数也被用来描述某些生物过程的变化规律，如种群数量的增长和衰减等。

三、打勾函数的魅力探索

打勾函数的魅力，还体现在其背后所蕴含的数学思想和美学价值上。它以一种简洁而优雅的方式，展示了数学中的对称美、和谐美以及变化美。在打勾函数的图像中，我们可以看到一种完美的平衡和协调，它既有上升的力量，又有下降的趋势；既有变化的可能，又有稳定的特征。这种平衡和协调，正是数学美学的重要体现。

同时，打勾函数也启示我们，数学不仅仅是枯燥的数字和公式，它还蕴含着丰富的思想和哲理。通过研究打勾函数，我们可以更加深入地理解数学中的优化问题、极限问题以及函数的变化规律等。这些思想和哲理，不仅可以帮助我们更好地解决数学问题，还可以为我们的生活和工作提供有益的启示和指导。

四、结语

打勾函数，这个听起来神秘而充满魅力的数学存在，不仅在数学研究中占据着重要地位，更在经济学、物理学等多个领域展现出了广泛的应用价值。它以一种简洁而优雅的方式，展示了数学中的对称美、和谐美以及变化美。通过研究打勾函数，我们可以更加深入地理解数学中的思想和哲理，为我们的生活和工作提供有益的启示和指导。

在未来的学习和研究中，让我们一起继续探索打勾函数的奥秘吧！无论是对于数学爱好者来说，还是对于需要运用数学工具解决实际问题的人来说，打勾函数都将是一个充满挑战和机遇的领域。让我们携手前行，在这个奇妙的数学世界中，共同追寻那些隐藏在数字背后的真理和美感吧！