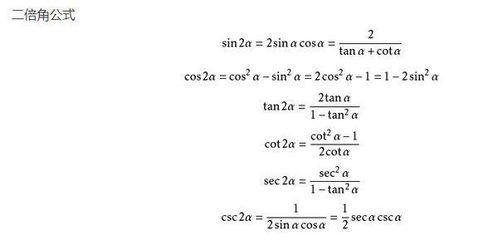等比数列求和公式的推导途径
在数学的世界里,等比数列作为一种特殊的数列类型,其求和公式的推导不仅是数列知识中的一大亮点,也是理解数列性质、掌握数学归纳法及代数运算技巧的重要途径。等比数列,顾名思义,是指从第二项起,每一项与它的前一项的比值等于同一个常数(不为0)的数列。这个常数我们称之为公比。等比数列求和公式的推导,虽然初看之下可能较为复杂,但通过逐步分解,我们可以清晰地看到其背后的逻辑之美。

等比数列求和公式的初步认识
等比数列求和公式表述为:对于一个首项为a1,公比为r的等比数列,其前n项和Sn可表示为:

当r ≠ 1时,Sn = a1(1 - r^n) / (1 - r);

当r = 1时,Sn = na1(因为此时每项都相等,直接相加即可)。
推导方法的探索
方法一:错位相减法
这是最常用的推导方法之一,通过构建一个新的数列,与原数列错位相减,从而简化求和过程。
1. 写出等比数列的前n项和:
Sn = a1 + a1r + a1r^2 + ... + a1r^(n-1)
2. 将上式两边同时乘以公比r:
rSn = a1r + a1r^2 + a1r^3 + ... + a1r^n
3. 将乘以公比后的式子与原式错位相减:
Sn - rSn = a1 - a1r^n
(1 - r)Sn = a1(1 - r^n)
4. 解出Sn(注意,这里r ≠ 1,因为当r=1时,分母为0,无法直接相除):
Sn = a1(1 - r^n) / (1 - r)
这个推导过程直观展示了错位相减法的魅力,通过简单的代数运算,将原本复杂的求和过程转化为一个简单的表达式。
方法二:数学归纳法
数学归纳法是一种证明与自然数有关的命题的常用方法,通过验证基础情况和归纳步骤来证明命题对所有正整数都成立。
1. 验证基础情况:
当n=1时,S1 = a1,显然满足公式Sn = a1(1 - r^n) / (1 - r)(因为r^1 ≠ 1时,(1 - r^1) / (1 - r) = 1,而当r=1时,由特殊情况直接得出S1=a1)。
2. 假设归纳假设:
假设当n=k时,公式成立,即Sk = a1(1 - r^k) / (1 - r)。
3. 证明归纳步骤:
考虑n=k+1时的情况,Sk+1 = Sk + ak+1 = a1(1 - r^k) / (1 - r) + a1r^k = a1(1 - r^k + r^k - r^(k+1)) / (1 - r) = a1(1 - r^(k+1)) / (1 - r)。
由此可见,当n=k+1时,公式依然成立。
4. 得出结论:
根据数学归纳法,公式对所有的正整数n都成立。
数学归纳法的推导虽然略显抽象,但它不仅证明了等比数列求和公式的正确性,还展示了数学证明中的一种重要思维方式——从特殊到一般,通过逐步推理达到普遍结论。
方法三:利用等比数列的性质
等比数列本身具有许多有趣的性质,利用这些性质也可以推导出求和公式。
1. 利用等比数列的通项公式:
对于等比数列,其通项公式为an = a1r^(n-1)。
2. 考虑等比数列的无限递减情况(r < 1且r ≠ 0):
如果我们将等比数列看作是一个无限递减的序列,并尝试求出其总和,会发现总和收敛于一个特定值。这可以通过无限几何级数求和的方法得出,但在此我们主要关注有限项和的情况。不过,这种思考方式有助于我们理解为何当|r| < 1时,等比数列的和会趋向于一个有限值。
3. 结合代数运算:
通过代数变换,我们可以将有限项和的表达式转化为上述错位相减法的形式,进而得出求和公式。这种方法在本质上与错位相减法相似,但更多地强调了等比数列性质的直接应用。
推导过程中的注意事项
1. 公比r的取值:
在推导过程中,需要特别注意公比r的取值。当r=1时,等比数列变为等差数列(每项都相等),求和公式直接简化为Sn=na1。而当|r| > 1时,等比数列的和可能迅速增大,需要特别注意其在实际应用中的限制。
2. 代数运算的准确性:
推导过程中涉及大量的代数运算,包括乘法、除法、指数运算等,需要确保每一步运算的准确性,避免因计算错误导致推导失败。
3. 理解推导背后的逻辑:
推导等比数列求和公式的过程,不仅是一次数学运算的练习,更是一次对数学逻辑、代数技巧以及数列性质深入理解的机会。因此,在推导过程中,应尝试理解每一步骤背后的逻辑,而不仅仅是机械地执行运算。
4. 联系实际应用:
等比数列求和公式在经济学、生物学、物理学等多个领域都有广泛应用。因此,在推导公式的同时,可以思考其在实际问题中的应用场景,这将有助于加深对公式的理解和记忆。
综上所述,等比数列求和公式的推导是一个既富有挑战性又充满趣味性的过程。通过不同的推导方法,我们可以从多个角度理解这一公式的来源和性质,从而在数学学习和实践中更加游刃有余。
- 上一篇: 如何轻松使用格式播放器打开视频文件
- 下一篇: 银行卡被吞了该怎么办?
-
 金字塔模型的具体公式是什么?资讯攻略11-14
金字塔模型的具体公式是什么?资讯攻略11-14 -
 半圆面积的计算公式是什么?资讯攻略10-29
半圆面积的计算公式是什么?资讯攻略10-29 -
 圆的面积计算公式是如何推导出来的?资讯攻略02-17
圆的面积计算公式是如何推导出来的?资讯攻略02-17 -
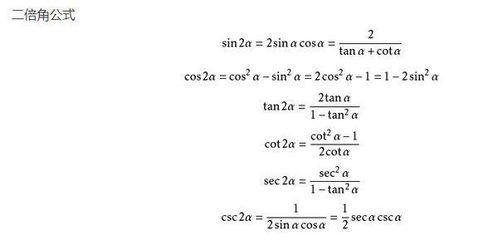 精通常见三角函数积分:公式推导与全面总结资讯攻略11-18
精通常见三角函数积分:公式推导与全面总结资讯攻略11-18 -
 等差与等比数列概览资讯攻略01-06
等差与等比数列概览资讯攻略01-06 -
 一维热传导方程详解资讯攻略11-15
一维热传导方程详解资讯攻略11-15