CNM排列组合公式的定义是什么

在数学领域中，排列与组合是计数问题中的重要概念，广泛应用于概率论、统计学、计算机科学等多个学科。当我们提到“cnm排列组合公式”时，实际上是指从n个不同元素中取出m个元素的所有排列与组合方式的计数方法。这里的“c”代表组合（Combination），“n”代表总数，“m”代表取出的数量，而排列（Permutation）虽然没有直接体现在这个缩写中，但它是与组合相对应的另一个重要概念。下面，我们就来详细探讨一下排列与组合的基本公式及其应用场景。

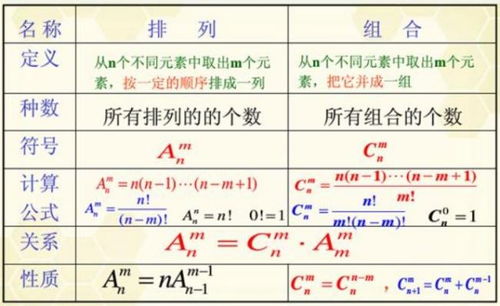
一、排列的概念与公式

排列是指从n个不同元素中取出m个元素（m≤n，且m与n均为自然数），按照一定的顺序排成一列。排列注重的是元素的顺序，即不同的排列顺序被视为不同的排列。

排列的公式：

P(n，m) = n! / (n-m)!

其中，P(n，m)表示从n个元素中取出m个元素的所有排列数，“!”表示阶乘，即n! = n × (n-1) × ... × 3 × 2 × 1。例如，从5个人中选3个人排成一队，其排列数为P(5，3) = 5! / (5-3)! = 5 × 4 × 3 = 60种。

二、组合的概念与公式

组合则是指从n个不同元素中取出m个元素（m≤n，且m与n均为自然数），不考虑取出元素的顺序。即，只要取出的元素相同，无论顺序如何，都视为同一种组合。

组合的公式：

C(n，m) = n! / [m!(n-m)!]

其中，C(n，m)表示从n个元素中取出m个元素的所有组合数。例如，从5个人中选3个人组成一个小组（不考虑小组内成员的排列顺序），其组合数为C(5，3) = 5! / [3!(5-3)!] = 5 × 4 / (3 × 2 × 1) = 10种。

三、排列与组合的区别与联系

1. 区别：

排列注重顺序，组合不注重顺序。

排列数通常大于或等于组合数，因为对于同一种组合，可以有多种排列方式。

2. 联系：

排列与组合都是基于“从n个不同元素中取出m个元素”这一前提。

排列数P(n，m)与组合数C(n，m)之间存在关系：P(n，m) = C(n，m) × m!。即，从n个元素中取出m个元素的排列数等于从n个元素中取出m个元素的组合数乘以m的阶乘。

四、排列组合公式的应用

排列组合公式在实际生活中有着广泛的应用，包括但不限于以下几个方面：

1. 概率计算：在概率论中，排列组合公式用于计算事件发生的可能性。例如，在抽奖活动中，计算中奖号码的排列组合数，从而确定中奖概率。

2. 密码学：在密码学中，排列组合原理被用于设计加密算法和破解密码。通过排列组合的方式，可以生成大量的密钥组合，提高密码的安全性。

3. 数据分析：在数据分析中，排列组合公式用于从大量数据中提取有用信息。例如，在市场调研中，通过排列组合的方式分析消费者的购买行为，为营销策略提供数据支持。

4. 计算机科学：在计算机科学中，排列组合原理被广泛应用于算法设计、数据结构优化等领域。例如，在搜索引擎中，通过排列组合的方式对关键词进行排序和匹配，提高搜索结果的准确性和相关性。

5. 游戏设计：在游戏设计中，排列组合原理被用于设计游戏关卡、角色属性等。通过排列组合的方式，可以生成丰富的游戏内容和多样的游戏体验。

五、排列组合公式的计算方法与优化

在计算排列组合数时，需要注意以下几点：

1. 避免重复计算：在计算排列组合数时，要确保每个元素只被计算一次，避免重复计算导致结果偏大。

2. 利用对称性：排列组合公式具有对称性，即C(n，m) = C(n，n-m)。在计算组合数时，可以利用这一性质简化计算过程。

3. 利用阶乘性质：在计算排列数时，可以利用阶乘的性质进行化简。例如，P(n，m) = n! / (n-m)! 可以化简为n × (n-1) × ... × (n-m+1)。

4. 使用递归算法：对于较大的n和m值，可以使用递归算法来计算排列组合数。递归算法通过将问题分解为更小的子问题来求解，从而提高计算效率。

5. 利用数学软件：在实际应用中，可以借助数学软件（如Matlab、Python等）来计算排列组合数。这些软件提供了丰富的数学函数和库函数，可以方便地实现排列组合数的计算。

六、总结

排列与组合是数学中的基本概念之一，它们在计数问题中发挥着重要作用。通过掌握排列组合的基本公式和计算方法，我们可以更好地理解和解决实际问题。同时，排列组合公式在概率论、统计学、计算机科学等多个学科中都有着广泛的应用价值。因此，在学习和实践中，我们应该注重理解和掌握排列组合的基本原理和方法，不断提高自己的数学素养和实际应用能力。