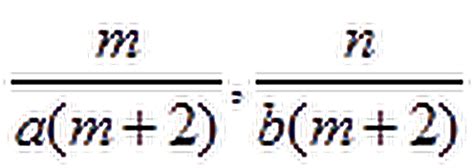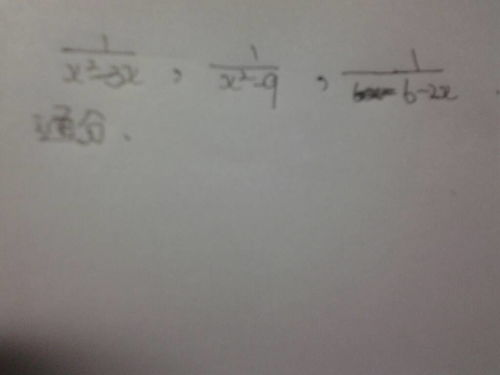如何轻松找到分式的最简公分母?
在数学的广阔天地里,分式运算以其独特的魅力和广泛的应用,成为了我们探索数学奥秘的必经之路。而在分式的加减运算中,一个至关重要而又常常让初学者感到困惑的问题,就是如何找到最简公分母。今天,就让我们一起揭开这个谜团,深入探讨如何高效、准确地找到分式的最简公分母。
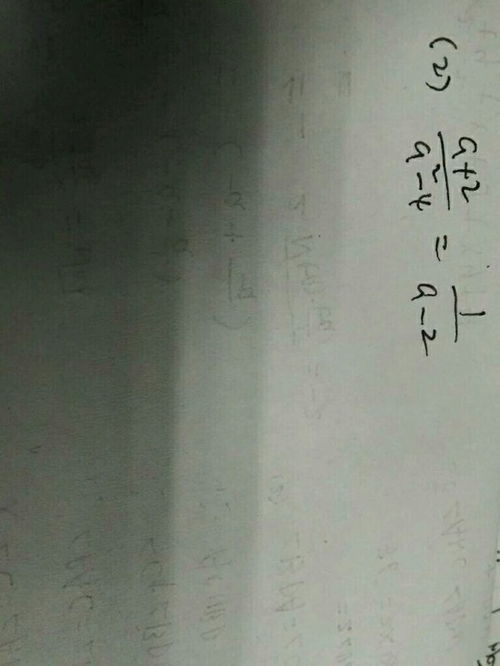
首先,我们需要明确什么是公分母。简单来说,当我们需要对两个或两个以上的分式进行加减运算时,为了统一这些分式的分母,就需要找到一个公共的分母,即公分母。而这个公分母,应当是所有分式分母的最小公倍数(LCM)。
那么,如何找到这个最小公倍数呢?这就需要我们运用到分解质因数的技巧。分解质因数,就是把一个合数分解成若干个质因数的乘积。例如,12可以分解为2×2×3,15可以分解为3×5。通过分解质因数,我们可以清晰地看到每个数包含的质因子及其次数,从而为找到最小公倍数打下基础。
具体到分式,我们需要对每个分式的分母进行质因数分解。比如,有两个分式$\frac{a}{2x}$和$\frac{b}{3x^2y}$,它们的分母分别是2x和3x²y。对这两个分母进行质因数分解,我们得到:
2x = 2 × x
3x²y = 3 × x × x × y
接下来,我们需要确定每个质因子的最高次数。在上面的例子中,质因子有2、3、x和y。其中,2的最高次数是1(因为只有一个2),3的最高次数也是1(因为只有一个3),x的最高次数是2(因为x出现了两次),y的最高次数是1(因为只有一个y)。
因此,将这些质因子及其最高次数相乘,我们就可以得到最小公倍数,也就是最简公分母:
LCM = 2^1 × 3^1 × x^2 × y^1 = 6x²y
现在,我们已经找到了最简公分母6x²y。接下来,我们就可以利用这个公分母对原分式进行通分,从而进行加减运算。
通分的过程,就是把每个分式转化为以最小公倍数为分母的形式。这通常需要我们进行乘法运算,使得每个分式的分母都变为最小公倍数。例如,对于上面的两个分式$\frac{a}{2x}$和$\frac{b}{3x^2y}$,我们可以这样进行通分:
$\frac{a}{2x} = \frac{a × 3xy}{2x × 3xy} = \frac{3axy}{6x²y}$
$\frac{b}{3x^2y} = \frac{b × 2}{3x^2y × 2} = \frac{2b}{6x²y}$
现在,两个分式已经通分为了以6x²y为分母的形式,我们就可以轻松地进行加减运算:
$\frac{3axy}{6x²y} + \frac{2b}{6x²y} = \frac{3axy + 2b}{6x²y}$
当然,在实际操作中,我们通常会省略中间的一些步骤,直接写出通分后的结果。但理解这些步骤背后的原理,对于掌握分式运算的精髓至关重要。
此外,还有一些特殊情况需要我们注意。比如,当分式的分母含有字母的指数时,我们需要确保在找最小公倍数时,每个字母的指数都取到最高值。又如,当分式的分母是多项式时,我们需要先对多项式进行因式分解,然后再按照上述方法找到最小公倍数。
除了这些基本技巧外,还有一些实用的策略可以帮助我们更快地找到最简公分母。比如,我们可以利用已有的数学工具或软件来辅助计算最小公倍数;或者,我们可以先尝试对分式的分母进行简化,以减少后续计算的复杂度。
总之,找到分式的最简公分母是进行分式加减运算的关键步骤之一。通过分解质因数、确定质因子的最高次数、相乘得到最小公倍数等方法,我们可以高效地找到最简公分母并进行通分运算。同时,注意特殊情况的处理和实用策略的应用,也可以帮助我们更好地掌握分式运算的技巧和方法。
最后,需要强调的是,虽然找到最简公分母是分式运算中的一个重要环节,但真正掌握分式运算还需要我们在实践中不断练习和总结。只有通过大量的练习和实践,我们才能更加熟练地运用这些技巧和方法,从而在数学的世界里畅游无阻。
希望这篇文章能够帮助那些对“分式怎么找最简公分母”感兴趣的朋友们解开疑惑、掌握技巧。在未来的数学探索之路上,愿你们能够勇往直前、不断进步!
- 上一篇: QQ好友删除教程:轻松几步告别不需要的联系人
- 下一篇: 如何删除自己在抖音上发布的作品
-
 怎样快速记住找最简公分母的口诀?资讯攻略12-03
怎样快速记住找最简公分母的口诀?资讯攻略12-03 -
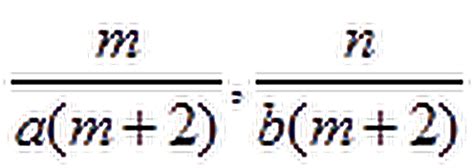 如何确定最简公分母的方法?资讯攻略01-26
如何确定最简公分母的方法?资讯攻略01-26 -
 如何确定最简公分母资讯攻略11-23
如何确定最简公分母资讯攻略11-23 -
 有理化分式的具体方法资讯攻略10-30
有理化分式的具体方法资讯攻略10-30 -
 怎样用最简方法折纸鹤?资讯攻略11-27
怎样用最简方法折纸鹤?资讯攻略11-27 -
 WPS中轻松掌握分数输入技巧资讯攻略02-11
WPS中轻松掌握分数输入技巧资讯攻略02-11