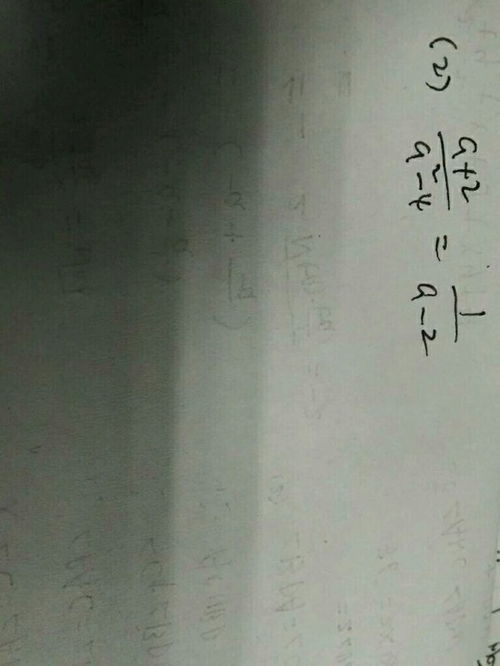有理化分式的具体方法

在数学领域，有理化是一项基本且重要的技能，尤其在处理无理数表达式时显得尤为重要。它主要是指通过一定的数学变换，将包含无理数的表达式转化为有理数的形式，从而简化计算或方便后续的数学处理。本文将围绕有理化的基本概念、具体方法以及应用场景展开详细介绍，旨在帮助读者掌握这一重要技能。

有理化的基本概念

有理数是可以表示为两个整数之比的数，而无理数则无法表示为两个整数的比。有理化通常指的是将包含根号（或其他形式无理数）的表达式进行变换，使其分母或整体转化为有理数。这种变换不仅在数学运算中能够简化问题，还可以帮助我们更清晰地理解数学表达式的本质。

有理化的基本方法

有理化的方法根据具体情况的不同而有所差异，但总体上可以分为两大类：分母有理化和分子有理化。下面分别介绍这两种方法。

分母有理化

分母有理化是最常见的有理化方法，主要用于处理分母包含根号或其他无理数的表达式。其基本思想是通过分子分母同时乘以某个适当的因子，使得分母中的无理数部分消失或转化为有理数。

示例一：

对于表达式$\frac{\sqrt{a} + b}{c + \sqrt{d}}$，我们可以通过分子分母同时乘以$c - \sqrt{d}$来进行有理化：

$\frac{\sqrt{a} + b}{c + \sqrt{d}} \times \frac{c - \sqrt{d}}{c - \sqrt{d}} = \frac{(\sqrt{a} + b)(c - \sqrt{d})}{c^2 - d}$

这样，分母就变成了一个有理数。

示例二：

对于更复杂的表达式，如$\frac{\sqrt{x+1} - \sqrt{x-1}}{\sqrt{x+2} + \sqrt{x-3}}$，有理化的过程可能会更复杂，但基本思想仍然是相同的：找到一个因子，使得分子分母同时乘以这个因子后，分母中的无理数部分消失。

分子有理化

分子有理化相对少见，但在某些特定情况下非常有用。它通常用于处理分子包含根号或其他无理数的表达式，通过乘以适当的因子，使得整个表达式变为有理数或更容易处理的形式。

示例：

对于表达式$\sqrt{x+1} - \sqrt{x-1}$，我们可以通过乘以共轭式$\sqrt{x+1} + \sqrt{x-1}$来进行分子有理化：

$(\sqrt{x+1} - \sqrt{x-1})(\sqrt{x+1} + \sqrt{x-1}) = (x+1) - (x-1) = 2$

有理化的应用场景

有理化在数学的许多领域都有着广泛的应用，包括但不限于以下几个方面：

1. 简化表达式

有理化可以极大地简化包含无理数的表达式，使其更易于理解和计算。这对于解决复杂的数学问题非常有帮助。

2. 求解方程

在解决某些类型的方程时，有理化是一个重要的步骤。例如，在求解含有根号的方程时，通常需要先进行有理化，然后再进行后续的计算。

3. 积分计算

在积分计算中，有理化也是一个常用的技巧。特别是当被积函数包含根号或其他无理数时，通过有理化可以将其转化为更容易积分的形式。

4. 几何问题

在某些几何问题中，有理化也是不可或缺的。例如，在解决与勾股定理相关的问题时，经常需要用到有理化的方法。

有理化的小技巧与注意事项

虽然有理化是一个相对简单的数学技巧，但在实际应用中还是需要注意一些细节和小技巧：

1. 选择合适的因子：在进行有理化时，选择合适的因子是非常关键的。一般来说，我们可以选择分母或分子的共轭式作为因子，这样可以确保有理化后的表达式更加简洁。

2. 检查符号：在进行有理化时，一定要注意符号的变化。特别是在处理复杂的表达式时，很容易因为符号错误而导致计算错误。

3. 避免过度复杂：虽然有理化可以简化表达式，但在某些情况下，过度复杂的有理化反而会使问题变得更加复杂。因此，在进行有理化时，我们需要根据具体情况来判断是否需要进行有理化以及如何进行有理化。

4. 保持耐心：有理化通常需要一些计算步骤和技巧，因此在解决问题时需要保持耐心和细心。特别是在处理复杂的表达式时，更需要耐心地进行计算和检查。

结语

有理化是数学中一个基本且重要的技能。通过掌握有理化的基本概念、具体方法以及应用场景，我们可以更好地理解和解决数学问题。无论是在简化表达式、求解方程、积分计算还是解决几何问题中，有理化都发挥着重要的作用。因此，我们应该注重培养和提高自己的有理