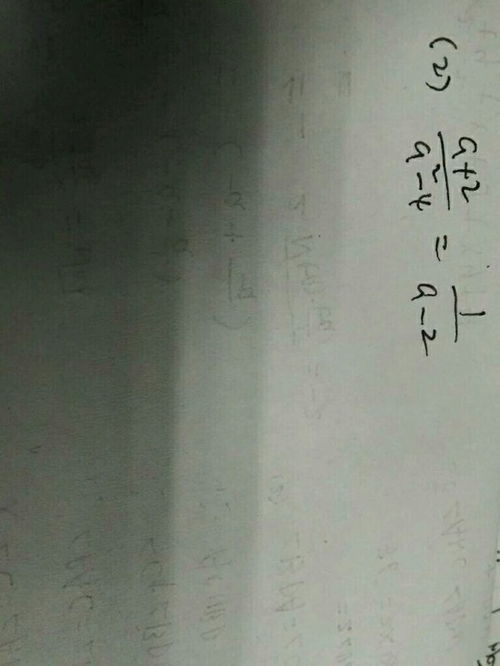揭秘：数学分式到底是什么？

在这个纷繁复杂的世界里，数学以其独特的语言，编织着宇宙的奥秘与日常的琐碎。它像一把无形的钥匙，解锁着自然界的密码，也为我们理解生活提供了有力的工具。而在数学的浩瀚宇宙中，有一个既神秘又实用的存在——分式，它如同一位低调而优雅的智者，静静地站在那里，等待着我们去探索它的智慧与魅力。

想象一下，当你面对一块美味的蛋糕，想要公平地分享给几位朋友时，你会怎么做？没错，你可能会将蛋糕切成若干等份，每个人得到其中的一份或几份。这个简单的行为背后，就隐藏着分式的概念。分式，简而言之，就是表示两个数相除的结果的数学形式，通常用“a/b”（读作“a分之b”）来表示，其中a是分子，b是分母，且b不能为0。它不仅是数学运算中的基础元素，更是连接整数、小数、百分数等多种数学形态的桥梁。

分式的诞生：从日常到抽象

分式的起源，可以追溯到人类最早对数量的认知与分配。在远古时代，人们就开始使用简单的分数来表示物品的部分与整体的关系。比如，猎人捕获了一头野兽，需要将肉平均分给部落成员，这时就需要用到分数来计算每个人应得的部分。随着时间的推移，分数逐渐从具体的实物分配抽象为数学上的概念，成为研究数量、比例、比例关系的重要工具。

分式的构成：分子与分母的故事

让我们深入分式的内部结构，一探究竟。分式由两部分组成：分子和分母。分子位于分数线之上，表示被除数；分母位于分数线之下，表示除数。这两个数字共同决定了分式的值。例如，在分式“3/4”中，3是分子，4是分母，它代表了“把1个整体分成4等份，取其中的3份”的意思。

值得注意的是，分式的分母不能为0。这是因为，在数学逻辑上，任何数除以0都是没有意义的，它会导致不确定的结果或数学上的“无穷大”。因此，当我们遇到分母为0的情况时，需要特别小心处理，通常意味着该分式是无定义的。

分式的运算：加减乘除的奥秘

分式的运算，是数学学习中不可或缺的一环。与整数和小数一样，分式也可以进行加减乘除等基本运算，但操作过程相对复杂，需要遵循一定的规则。

加法与减法：在进行分式的加减运算时，首先要找到两个分式的“公共分母”。只有当分母相同时，分子才能进行直接的加减。如果分母不同，就需要通过“通分”的方法，将两个分式转化为具有相同分母的形式。例如，“1/2 + 1/3”需要先转化为“3/6 + 2/6”，然后再进行加法运算，得到“5/6”。

乘法与除法：分式的乘法相对简单，只需将两个分式的分子相乘，分母相乘即可。如“(2/3) × (4/5)”直接计算为“8/15”。而分式的除法，则需要将除数取倒数，然后与被除数相乘。例如，“(2/3) ÷ (4/5)”可以转化为“(2/3) × (5/4)”，结果为“10/12”，进一步化简为“5/6”。

分式的应用：从生活到科学的跨越

分式的魅力，不仅仅在于其运算规则的美妙，更在于它在实际生活中的广泛应用。从日常的购物打折、烹饪食谱的比例调配，到科学领域的物理公式、化学反应速率计算，分式无处不在。

日常生活：在购物时，我们经常会遇到打折促销的情况。比如，“全场商品五折优惠”，这里的“五折”就是一个分式，表示原价的50%，即“1/2”。在烹饪中，食谱上的“两杯面粉配一杯水”也是分式的应用，它确保了食物的口感和质地。

教育领域：在学习物理时，分式帮助我们理解速度（距离/时间）、加速度（速度变化量/时间）等概念。在化学中，反应速率（反应物消耗量/时间）的计算同样离不开分式。甚至在经济学里，利率、增长率等经济指标的计算，也频繁使用分式来表达和分析。

科学探索：在更深的科学层面，分式在微积分、概率论、复变函数等领域发挥着至关重要的作用。它们是解决复杂问题、建立数学模型的基础工具，帮助科学家们探索宇宙的奥秘，揭示自然的规律。

分式的魅力：从简单到复杂的探索之旅

分式的魅力，还在于它能够引导我们从简单到复杂，逐步深入数学的殿堂。从最初的认识分式、理解其基本概念，到掌握分式的运算规则，再到将其应用于实际问题解决，每一个步骤都是一次思维的跳跃，一次智慧的成长。

在这个过程中，我们学会了如何将复杂问题分解为简单部分，如何运用逻辑和推理来解决问题，如何从不同角度审视同一个问题