揭秘分式的本质定义
在数学的浩瀚宇宙中,分式作为一座独特的桥梁,连接着数与式的广阔天地,以其独特的形态和深刻的内涵,在代数、几何乃至更广泛的数学领域中发挥着不可或缺的作用。本文旨在从多个维度深入剖析分式的定义,探讨其性质、应用及与数学其他分支的关联,以期为读者呈现一个全面而生动的分式世界。

一、分式的定义与基本形态
分式,简而言之,是表示两个整式之间除法关系的式子,其一般形式为$\frac{P(x)}{Q(x)}$,其中$P(x)$和$Q(x)$为整式,且$Q(x) \neq 0$。这个定义直观地告诉我们,分式由分子($P(x)$)和分母($Q(x)$)两部分组成,分母不能为零,这是分式存在的基本前提,也是避免数学上无意义运算的关键。
从形式上看,分式是对整数除法概念的推广和深化。在整数除法中,被除数除以除数得到商;而在分式中,分子整式除以分母整式,得到的结果是一个新的数学对象——分式。这种推广不仅扩大了数的范围,还赋予了数学表达更丰富的层次和深度。
二、分式的性质与运算
分式的性质是理解其本质和应用的基础。首先,分式具有等价性,即如果两个分式的分子分母对应成比例(且比例不为零),则这两个分式等价。这一性质为分式的化简提供了理论依据,也是解决分式方程和不等式的基础。
其次,分式的运算规则遵循基本的算术运算规律,但需注意分母不为零的限制。加法、减法、乘法和除法在分式中的应用,需要借助通分、约分等技巧,确保运算的有效性和准确性。特别是分式的乘除法,直接通过分子乘分子、分母乘分母的方式实现,而加减法则需先通分,再进行相应的算术运算。
此外,分式还具有一些特殊的性质,如倒数的性质(一个分式的倒数是将其分子分母互换位置得到的分式)、分式与整数的互化等,这些性质在解决复杂数学问题时往往能发挥关键作用。
三、分式的应用实例
分式的应用领域广泛,几乎渗透到数学的每一个角落。在代数中,分式方程和不等式是解决实际问题的有效工具,如物理中的运动学问题、经济学中的增长率问题,常可通过建立分式方程来求解。
在几何学中,分式用于描述图形的比例关系,如相似三角形的边长比、圆的切线长与半径的关系等,分式的引入使得几何问题的解决更加精确和高效。
在函数论中,分式函数(如有理函数)是重要的研究对象,它们的图像、单调性、极值等性质,对于理解函数的本质特征具有重要意义。特别是在复分析中,分式函数与莫比乌斯变换紧密相关,成为研究复平面变换的强大工具。
此外,在概率论、统计学、物理学等多个领域,分式也扮演着重要角色,如概率的计算、统计量的构建、物理公式的推导等,分式的存在使得这些领域的问题得以更加精确地描述和解决。
四、分式与数学其他分支的关联
分式作为数学体系中的一个基本元素,与其他数学分支之间存在着千丝万缕的联系。在代数领域,分式与多项式、方程、不等式等概念相互交织,共同构建了代数理论的基石。在微积分中,分式函数是导数、积分计算中的重要对象,其极限行为、单调性、最值等问题,是微积分研究的重点之一。
在数论中,虽然分式不是直接研究对象,但分数形式的表示对于理解有理数、素数分布、费马小定理等概念有着不可忽视的作用。在组合数学中,分式常用于计数问题的概率计算,如二项式定理、斯特林数等的表达,分式形式的引入使得计数问题得以更加简洁地解决。
特别值得一提的是,在复数域中,分式的应用更加广泛而深刻。复数的除法运算实质上是分式的运算,复平面上的莫比乌斯变换、黎曼球面等概念,都是基于分式的深刻理解和应用。这些关联不仅展示了分式的普适性和强大功能,也揭示了数学内部各分支之间的深刻联系和统一性。
五、分式教育意义与启示
分式的教学,不仅仅是知识的传授,更是思维方式的训练。通过学习分式,学生可以学会如何将复杂问题转化为简单问题,如何运用已知条件进行逻辑推理,如何在变化中寻找不变的本质。这些能力和素养,对于学生未来的学习和生活都将产生深远的影响。
同时,分式的学习也提醒我们,数学不仅仅是数字和符号的游戏,它更是一种探索世界、理解自然的工具。在数学的世界里,每一个概念、每一个定理,都是人类智慧的结晶,它们之间存在着错综复杂而又和谐统一的关系。通过学习分式,我们可以更加深刻地体会到
- 上一篇: 个税计算方法及公式全解析
- 下一篇: NBA季后赛分组规则是怎样的?
-
 揭秘:数学分式到底是什么?资讯攻略11-08
揭秘:数学分式到底是什么?资讯攻略11-08 -
 如何轻松找到分式的最简公分母?资讯攻略11-27
如何轻松找到分式的最简公分母?资讯攻略11-27 -
 有理化分式的具体方法资讯攻略10-30
有理化分式的具体方法资讯攻略10-30 -
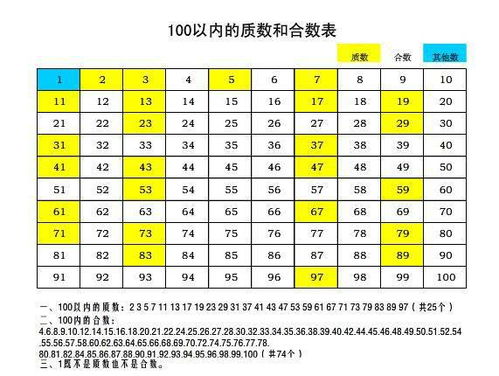 揭秘:奇数的定义与特性资讯攻略12-02
揭秘:奇数的定义与特性资讯攻略12-02 -
 样本空间的定义与解析资讯攻略11-20
样本空间的定义与解析资讯攻略11-20 -
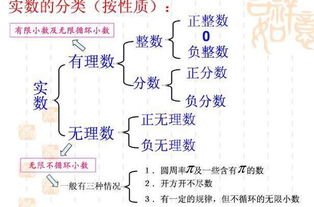 有理数的定义及实例解析资讯攻略10-25
有理数的定义及实例解析资讯攻略10-25