如何计算扇形的弧长
在数学的浩瀚宇宙中,扇形以其独特的形态和性质,成为了几何学领域一颗璀璨的星辰。扇形,作为圆的一部分,由圆的两条半径和这两条半径之间的一段弧所围成,它不仅承载着圆的美学与和谐,还蕴含着丰富的数学原理和计算技巧。本文将深入探讨如何求解扇形的弧长,从定义理解、公式推导、实例应用以及实际生活中的关联等多个维度,为读者揭开扇形弧长的神秘面纱。

一、扇形弧长的定义
扇形弧长,顾名思义,指的是扇形中那段由圆心角决定的曲线段的长度。它连接了扇形的两个端点,是扇形不可或缺的一部分。理解扇形弧长的概念,首先需要明确圆心角的概念。圆心角是以圆心为顶点的角,其度数大小直接决定了扇形面积和弧长的大小。一般而言,整个圆的圆心角为360度(或2π弧度),而扇形的圆心角则是其中的一部分。

二、扇形弧长公式的推导
扇形弧长的计算依赖于圆心角和圆的半径。要找到这两者之间的关系,我们得回到弧度制的本质。弧度制是度量角的一种方式,与度数制不同,它使得角度与弧长之间建立了直接的比例关系。具体来说,弧长(L)与圆心角(θ,以弧度为单位)和半径(r)之间的关系可以表示为:
L = θ × r
这个公式的推导可以从圆的周长出发。圆的周长公式为C = 2πr,如果我们将整个圆看作一个圆心角为2π弧度的扇形,那么整个圆的周长就等价于圆心角为2π的扇形的弧长。由此,对于任意圆心角的扇形,其弧长即可通过上述比例关系得出。
三、扇形弧长的实例应用
掌握扇形弧长的计算方法后,我们可以将其应用于解决各类实际问题。例如,在设计制造车轮时,为了确保车轮行驶平稳,减少振动,车轮上的每个辐条都需要均匀分布,这涉及到计算车轮圆周上特定位置与轮毂之间的弧长。又如在制作扇形窗棂或装饰品时,需要根据设计要求准确计算出扇形的弧长,以确保材料的使用既不过剩也不短缺。
案例一:计算自行车辐条长度
假设自行车轮毂半径为30厘米,需要计算辐条从轮毂中心到轮缘(假设轮缘为一个圆周上的点)的弧长。若辐条与轮毂中心的连线与水平轴夹角为45度(转换成弧度约为π/4),则辐条对应的扇形弧长为:
L = (π/4) × 30 ≈ 23.55厘米
案例二:制作扇形窗棂
如果要制作一个半径为50厘米,圆心角为90度(即π/2弧度)的扇形窗棂,那么其弧长为:
L = (π/2) × 50 = 78.54厘米
通过这些实例,我们可以深刻体会到扇形弧长计算在现实生活中的应用价值。
四、扇形弧长与生活的联系
扇形不仅在数学题目中频繁出现,它与我们的日常生活也息息相关。从钟表指针的运动轨迹到扇形图表的直观展示,从遮阳伞的张开形状到水果切片的摆放方式,扇形无处不在,而弧长作为扇形的核心属性之一,同样影响着这些现象的解读和应用。
1. 钟表指针的旅行
每一分钟,钟表的时针和分针都在以固定的圆心角移动,这种移动轨迹正是扇形弧长的体现。通过观察指针移动的弧长,我们可以精确地读取时间。
2. 扇形图表的魅力
在数据分析中,扇形图表(即饼图)被广泛用于展示各部分占总体的比例。每一个扇形区块的大小,正是由其对应的圆心角和半径决定的弧长所决定的,使得信息可视化变得直观且易于理解。
3. 自然界的扇形现象
自然界的许多事物也呈现扇形结构,如扇贝的壳、孔雀开屏的形态等。虽然这些自然现象背后的数学原理可能更为复杂,但弧长作为构成扇形美的基础元素,依然在这些美丽的形态中发挥着不可或缺的作用。
五、进一步探索:弧长与面积的关联
在深入了解扇形弧长的同时,我们不能忽视它与扇形面积之间的内在联系。扇形面积的计算公式为:
S = (1/2) × θ × r^2
与弧长公式相比,面积公式多了一个半径的平方项,这反映了面积作为二维量度,相较于一维的弧长,更多地考虑了半径带来的扩展效应。但无论是弧长还是面积,圆心角θ和半径r都是决定它们大小的关键因素。通过比较弧长与面积的计算过程,我们可以更好地理解圆的几何特性和微积分在解决几何问题中的应用。
结语
扇形弧长的求解,不仅仅是数学运算的简单应用,更是对几何学深刻理解的一种体现。它让我们得以从微小的弧度中窥见圆的奥秘,从生活中的点点滴滴中感受到数学的魅力。从圆心角的确定到弧长的计算,每一步都充满了探索的乐趣和智慧的火花。通过对扇形弧长的全面探索,我们不仅提升了数学能力,也深化了对这个世界的认知,感受到了数学与现实世界的和谐统一。
- 上一篇: 安卓手机微信聊天记录存储位置
- 下一篇: 家常美味必学:蒜苗回锅肉的绝妙做法
-
 高中扇形弧长与面积计算公式详解资讯攻略11-10
高中扇形弧长与面积计算公式详解资讯攻略11-10 -
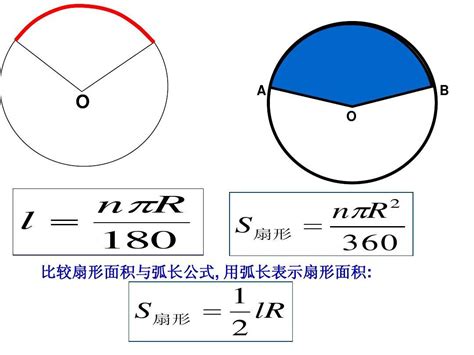 扇形面积如何计算?资讯攻略11-27
扇形面积如何计算?资讯攻略11-27 -
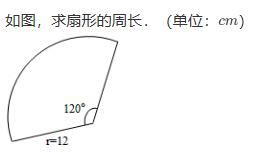 如何计算扇形的周长资讯攻略02-26
如何计算扇形的周长资讯攻略02-26 -
 掌握第一类曲线积分的高效计算方法资讯攻略11-01
掌握第一类曲线积分的高效计算方法资讯攻略11-01 -
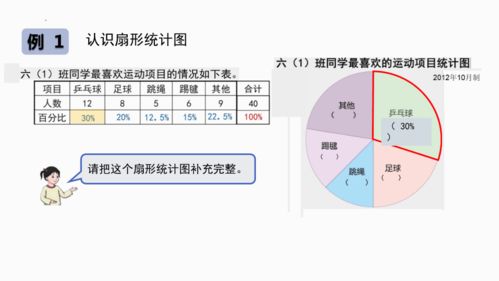 如何制作PPT中的扇形统计图资讯攻略11-15
如何制作PPT中的扇形统计图资讯攻略11-15 -
 Excel制作扇形统计图的简单步骤资讯攻略11-10
Excel制作扇形统计图的简单步骤资讯攻略11-10












