概率与统计的计算方法
在探索数据的奥秘时,概率和统计是两个不可或缺的工具。它们为我们提供了一种理解和分析随机现象、预测未来趋势以及从数据中提取有价值信息的方法。无论是科学研究、商业决策还是日常生活,掌握如何计算概率和进行统计分析都显得至关重要。

首先,让我们从概率的基本概念谈起。概率是衡量某一事件发生的可能性的数值。其值介于0和1之间,其中0表示事件不可能发生,1表示事件一定会发生。计算概率的基本公式是“事件发生的次数除以所有可能事件的总次数”。例如,抛掷一枚公平的六面骰子,某一特定数字(如6)朝上的概率是1/6,因为每个数字朝上的机会是均等的,总共有6种可能的结果。

在更复杂的情境中,我们可能会遇到复合事件,即涉及多个简单事件组合的情况。这时,我们需要用到概率的加法定理和乘法定理。加法定理指出,如果两个事件是互斥的(即不能同时发生),那么这两个事件中至少有一个发生的概率等于它们各自发生的概率之和。乘法定理则用于计算两个事件同时发生的概率,其公式是两个事件各自发生的概率的乘积,但前提是这两个事件是相互独立的,即一个事件的发生不影响另一个事件的发生概率。

条件概率是另一个重要的概念,它指的是在已知某个事件已经发生的情况下,另一个事件发生的概率。计算条件概率需要使用条件概率公式,即“在A发生的条件下B发生的概率等于A和B同时发生的概率除以A发生的概率”。条件概率在决策分析、贝叶斯定理等高级统计应用中扮演着关键角色。
接下来,我们转向统计学的世界。统计学是研究如何收集、整理、分析和解释数据的科学。它提供了一套系统的工具和方法,帮助我们从大量的数据中提取有用的信息,并做出合理的推断。统计分析通常包括描述性统计和推断性统计两部分。
描述性统计侧重于对数据的描述和总结,通过计算各种统计量(如均值、中位数、众数、方差、标准差等)来概括数据的特征。均值是衡量数据集中趋势的指标,中位数则不受极端值的影响,能更好地反映数据的中心位置。方差和标准差则用于衡量数据的离散程度,即数据点之间的波动大小。
推断性统计则允许我们从样本数据推断出总体参数的信息。由于在实际研究中,我们往往无法直接观测到整个总体,而只能获取到总体的一个样本,因此需要通过样本数据来估计总体的特征。这里涉及到两个重要的概念:置信区间和假设检验。置信区间给出了总体参数估计的可靠范围,而假设检验则用于检验我们对总体参数的某个假设是否成立。
在计算置信区间时,我们通常会选择一个置信水平(如95%),这表示我们有95%的信心认为总体参数落在我们计算出的置信区间内。置信区间的计算依赖于样本的大小、样本数据的分布以及所选择的置信水平。
假设检验则是基于一定的假设(即原假设),通过样本数据来检验这个假设是否成立。其基本步骤包括提出假设、确定检验统计量、计算检验统计量的值、确定拒绝域以及根据计算出的统计量值与拒绝域的关系做出决策。常见的假设检验类型包括单样本t检验、双样本t检验、卡方检验等,它们适用于不同的数据类型和研究情境。
在实际应用中,概率和统计经常是相互交织的。例如,在风险评估中,我们需要计算某一不利事件发生的概率,并基于这个概率来评估其可能造成的损失和影响。在市场调研中,我们可能会利用统计方法来分析消费者的购买行为,从而预测未来的市场趋势和需求变化。在金融领域,概率和统计更是无处不在,它们被用于投资组合的优化、信用评分的计算以及市场风险的管理等方面。
此外,随着大数据和人工智能技术的快速发展,概率和统计在数据分析中的作用日益凸显。大数据分析往往涉及海量的数据和复杂的模型,而概率和统计为我们提供了处理这些数据、提取有用信息以及做出准确预测的方法。在机器学习中,概率和统计更是基础中的基础,它们被用于模型的训练、特征的提取以及结果的评估等方面。
总之,概率和统计是数据分析和决策制定中不可或缺的工具。它们为我们提供了一种科学的方法来理解和分析随机现象、预测未来趋势以及从数据中提取有价值的信息。无论是在学术研究、商业决策还是日常生活中,掌握这些技能都将使我们能够更好地应对各种挑战和机遇。因此,我们应该不断学习和实践这些技能,以提升自己的数据素养和决策能力。
- 上一篇: 小米账号轻松注册指南:一步步教你搞定!
- 下一篇: 十大智商最高的犬种排行
-
 掌握数学新境界:【在线GeoGebra高效运用指南】资讯攻略11-24
掌握数学新境界:【在线GeoGebra高效运用指南】资讯攻略11-24 -
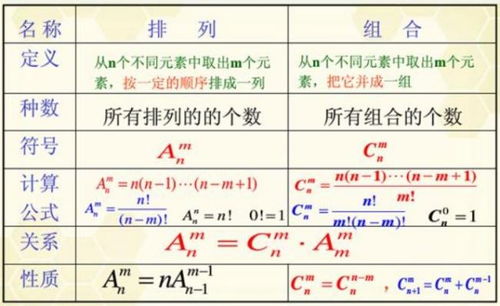 CNM排列组合公式的定义是什么资讯攻略11-26
CNM排列组合公式的定义是什么资讯攻略11-26 -
 地震基本烈度与设防烈度的定义及区别资讯攻略11-06
地震基本烈度与设防烈度的定义及区别资讯攻略11-06 -
 揭秘概率世界的五大基石:深度解析概率运算核心公式资讯攻略10-27
揭秘概率世界的五大基石:深度解析概率运算核心公式资讯攻略10-27 -
 卡西欧计算器计算方差的方法资讯攻略10-31
卡西欧计算器计算方差的方法资讯攻略10-31 -
 解锁数据奥秘:全面汇总资料分析必备公式资讯攻略11-01
解锁数据奥秘:全面汇总资料分析必备公式资讯攻略11-01












