揭秘正方形对角线的神奇性质
正方形作为几何学中一种基本而重要的形状,其独特的性质一直是数学家和几何学者研究的热点。在众多性质中,正方形对角线的性质尤为引人注目。正方形对角线不仅长度相等,而且互相垂直平分,同时它们还将正方形划分为两个全等的等腰直角三角形。这些性质不仅在数学领域有广泛应用,而且在建筑、工程和设计等领域也扮演着重要角色。

正方形对角线的基本性质之一,是它们的长度相等。这一性质源于正方形的定义:一个所有边都相等的四边形。由于正方形的四条边都相等,因此其对角线必然也相等。这一性质的证明可以通过简单的几何构造来完成。设正方形ABCD,其中AB=BC=CD=DA,那么其对角线AC和BD的长度可以通过勾股定理来计算。设正方形的边长为a,则AC和BD的长度均为根号2倍的a,即AC=BD=√2a。这一性质在解决与正方形相关的几何问题时非常有用,它可以帮助我们快速确定正方形的对角线长度。
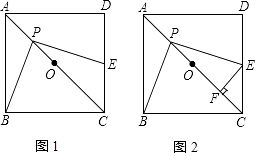
除了长度相等外,正方形对角线还互相垂直平分。这一性质是正方形对称性的体现。在正方形中,对角线不仅将正方形划分为两个全等的等腰直角三角形,而且它们还互相垂直。这一性质的证明可以通过几何构造和逻辑推理来完成。设正方形ABCD,其对角线AC和BD相交于点O。由于正方形的对称性,我们可以得出AO=OC,BO=OD。同时,由于正方形的内角都是直角,所以∠AOB=∠BOC=∠COD=∠DOA=90°。这证明了正方形对角线互相垂直平分。这一性质在几何证明和计算中非常有用,它可以帮助我们确定正方形的中心点和对称轴。

正方形对角线还将正方形划分为两个全等的等腰直角三角形。这一性质是正方形对角线性质的一个重要推论。在正方形中,由于对角线互相垂直平分,因此它们将正方形划分为两个全等的等腰直角三角形。这两个三角形的两条直角边分别等于正方形的边长,而斜边则等于正方形的对角线。这一性质在解决与正方形和等腰直角三角形相关的几何问题时非常有用,它可以帮助我们快速确定三角形的边长和角度。
正方形对角线的性质在建筑、工程和设计等领域也有广泛应用。在建筑中,正方形对角线可以帮助建筑师确定建筑物的中心点和对称轴,从而确保建筑物的对称性和美观性。在工程中,正方形对角线可以帮助工程师计算结构的稳定性和强度,从而确保工程的安全性和可靠性。在设计中,正方形对角线可以帮助设计师确定设计的比例和尺寸,从而创造出更加美观和实用的设计作品。
此外,正方形对角线的性质还与一些数学定理和公式密切相关。例如,勾股定理是连接正方形对角线长度与其边长之间关系的重要定理。它表明,在直角三角形中,直角边的平方和等于斜边的平方。对于正方形对角线来说,这一定理可以表示为AC²=AB²+BC²(或BD²=AB²+AD²),其中AC和BD是正方形的对角线,AB、BC、AD是正方形的边长。这一公式在解决与正方形和直角三角形相关的几何问题时非常有用。
另外,正方形对角线的性质还与一些数学概念和性质有关。例如,正方形的对角线是其外接圆的直径。这一性质表明,正方形的外接圆是一个以正方形对角线为直径的圆。这一性质在解决与正方形和圆相关的几何问题时非常有用。同时,正方形的对角线也是其内切圆的切线。这一性质表明,正方形的内切圆是一个与正方形各边都相切的圆,而正方形的对角线则是这个圆的切线。这一性质在解决与正方形和圆相切的几何问题时也非常有用。
此外,正方形对角线的性质还与一些几何变换和对称性质有关。例如,正方形是关于其对角线对称的轴对称图形。这一性质表明,正方形可以通过其对角线进行轴对称变换而不改变其形状和大小。这一性质在解决与正方形和对称性质相关的几何问题时非常有用。同时,正方形也是关于其中心点中心对称的图形。这一性质表明,正方形可以通过其中心点进行中心对称变换而不改变其形状和大小。这一性质在解决与正方形和中心对称性质相关的几何问题时也非常有用。
综上所述,正方形对角线的性质是几何学中一个非常重要而有趣的话题。它们不仅在数学领域有广泛应用,而且在建筑、工程和设计等领域也扮演着重要角色。通过深入研究正方形对角线的性质,我们可以更好地理解正方形的本质特征,从而更好地应用它们来解决实际问题。同时,正方形对角线的性质也为我们提供了一种独特的视角来审视和理解几何学中的对称性和美感。
- 上一篇: 揭秘:高效解决便秘的神奇方法!
- 下一篇: 清新裸妆打造步骤图解指南
-
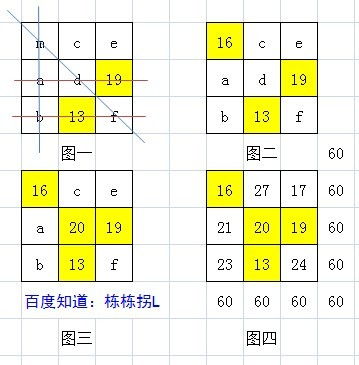 揭秘三阶幻方的神奇规律资讯攻略11-21
揭秘三阶幻方的神奇规律资讯攻略11-21 -
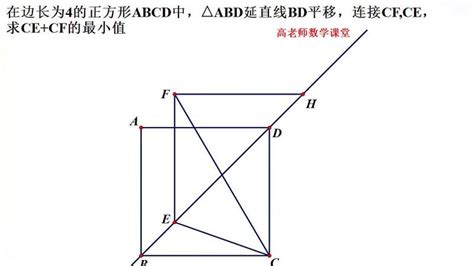 正方形对角线长度的简单计算方法资讯攻略12-01
正方形对角线长度的简单计算方法资讯攻略12-01 -
 揭秘!正方形周长的神奇计算公式,一看就会资讯攻略10-31
揭秘!正方形周长的神奇计算公式,一看就会资讯攻略10-31 -
 揭秘!酸的五大神奇化学性质及其经典反应方程式,让你秒懂酸碱奥秘资讯攻略10-26
揭秘!酸的五大神奇化学性质及其经典反应方程式,让你秒懂酸碱奥秘资讯攻略10-26 -
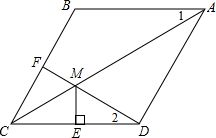 菱形边长求解对角线方法资讯攻略11-19
菱形边长求解对角线方法资讯攻略11-19 -
 揭秘二次根式性质的奥秘资讯攻略11-19
揭秘二次根式性质的奥秘资讯攻略11-19









